Idem para as vigas com rótulas internas representadas na figura seguinte:
 ii)
ii)
Passo 1
Ao considerarmos as reações de apoio, devemos considerar as reações no diagrama de corpo livre apresentado abaixo.
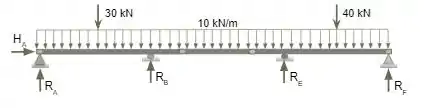 Para realizar as reações de apoio devemos considerar que:
Para realizar as reações de apoio devemos considerar que:
Passo 2
Como está esta viga possui duas rótulas interna, devemos separá-las nestes pontos e determinar um apoio fictício, separando-as em vigas isostáticas distintas.

Após isso substituiremos os apoios fictícios por forças contrárias nas vigas, representando o apoio de uma em outra.
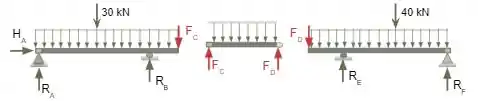
Passo 3
Começaremos então pela segunda parte da viga, representada abaixo.
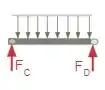
Ao substituirmos o valor de FD, na equação encontrada no somatório de forças da horizontal descobriremos o valor de FC e poderemos continuar resolvendo a primeira parte da viga.
Passo 4
Agora realizaremos os cálculos da primeira parte da viga, ilustrada logo abaixo.
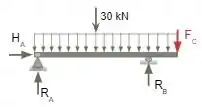
Devemos considerar FC como o valor encontrado acima, então FC=9,5 kN.
Substituindo o valor de RB na equação encontrada no equilíbrio horizontal, temos:
Passo 5
Para finalizar realizaremos os cálculos da terceira parte da viga, representada logo abaixo.
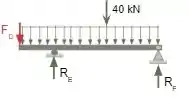 Nesta viga também devemos considerar o valor de FD igual ao encontrado anteriormente, então FD=9,5kN Realizando o equilibro de forças horizontais temos:
Nesta viga também devemos considerar o valor de FD igual ao encontrado anteriormente, então FD=9,5kN Realizando o equilibro de forças horizontais temos:
Substituindo o valor de RF na equação encontrada no equilíbrio de forças horizontais, teremos:
Resposta
3. ii)