Idem para as vigas com rótulas internas representadas na figura seguinte:
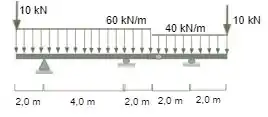 iv)
iv)
Passo 1
Ao considerarmos as reações de apoio, devemos considerar as reações no diagrama de corpo livre apresentado abaixo.
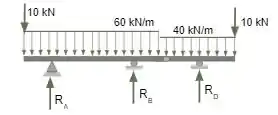 Nesta viga, não possuimos reações no sentido vertical, sendo assim consideramos este equílibrio automaticamente como zero. Para realizar as reações de apoio devemos considerar que:
Nesta viga, não possuimos reações no sentido vertical, sendo assim consideramos este equílibrio automaticamente como zero. Para realizar as reações de apoio devemos considerar que:
Passo 2
Como está esta viga possui uma rótula interna, devemos separá-la neste ponto e determinar um apoio fictício, separando-as em vigas isostáticas distintas.
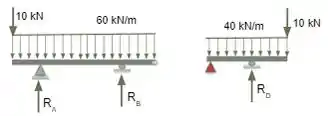
Após isso substituiremos os apoios fictícios por forças contrárias nas vigas, representando o apoio de uma em outra.
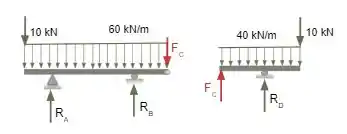
Passo 3
Começaremos então pela segunda parte da viga, representada abaixo.
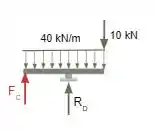
Agora para o equilibro de momentos no primeiro apoio, temos:
Ao substituirmos o valor de RD, na equação encontrada no somatório de forças da horizontal descobriremos o valor de RD e poderemos continuar resolvendo o restante da viga.
Passo 4
Agora realizaremos os cálculos da primeira parte da viga, ilustrada logo abaixo.
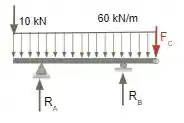
Devemos considerar FB como o valor encontrado acima, então FC= 180kN.
Agora para o equilibro de momentos no primeiro apoio, temos:
Substituindo o valor de RD na equação encontrada no equilíbrio horizontal, temos:
Resposta
3. iv)