Se a massa de 100 kg tem uma velocidade para baixo de ao passar pela sua posição de equilíbrio, calcule a magnitude de sua aceleração máxima. Cada uma das duas molas tem uma rigidez .
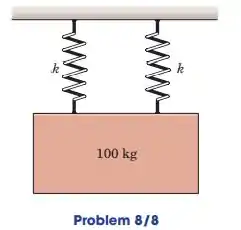
Passo 1
Falaaaai galerinha, show de bola? Bora resolver mais uma juntinho comigo?
Simboráaa
Já vamos iniciar com o noddo diagrama de corpo livre
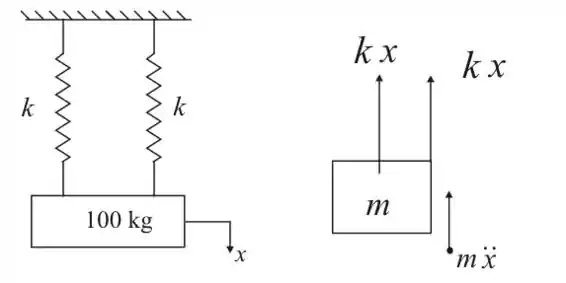
Passo 2
Temos um dado importante que e
Velocidade máxima
Deixando a massa ser deslocada da posição de equilíbrio e a equação de movimento liberada
Então a frequência natural do sistema acima é
Passo 3
A solução pra a expressão a seguir é
Podemos escrever como
A velocidade
Aceleração
Partindo da expressão de velocidade máxima é
E
Aceleração máxima
Resposta
Portanto, a velocidade máxima ocorre ao passar da posição de equilíbrio.