Uma massa se move em uma dimensão e está sujeita a uma força constante quando e a uma força constante , quando . Descreva o movimento construindo um diagrama de fase. Calcule o período do movimento em termos de , , e a amplitude, (desconsidere o amortecimento).
Passo 1
Então, galera, tudo tranquilo? Essa questão não é difícil, com calma vamos conseguir, vem comigo.
Primeiro vamos escrever a segunda lei de Newton para o movimento:
Com as condições iniciais , chegamos na solução:
Isolando o na expressão de
Mas precisamos de , vamos fazer então a substituição necessária, para chegar em:
Passo 2
Agora só precisamos plotar o gráfico de
O que resulta em uma parábola cujo vértice está sobre o ponto com coordenadas
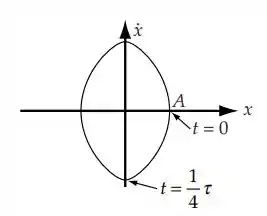
Passo 3
O período podemos calcular da seguinte forma:
Primeiro qual será o tempo para a partícula ir de até
O período equivale a quatro vezes o tempo acima:
Resposta
DEMONSTRAÇÃO