Uma massa M se move horizontalmente ao longo de um trilho liso. Um pêndulo está pendurado de M com uma haste sem peso e massa m, em sua extremidade. Encontre as frequências e descreva os modos normais.
Passo 1
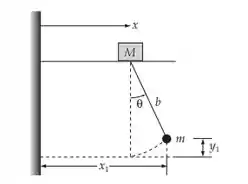
Portanto:
Para pequenos , Substituindo:
Passo 2
Portanto:

Devemos resolver:
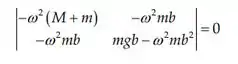
Que nos dá:

Passo 3
Substituindo na equação, temos:
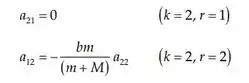
Portanto as equações:
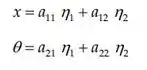
Se tornam:
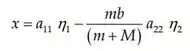
![]()
Passo 4
Resolvendo:
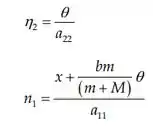
ocorre quando
ocorre quando
Resposta
Ei, a resposta está no passo a passo :)