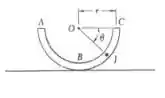
Meia seção de um tubo, com peso P e comprimento unitário, repousa sobre uma superfície horizontal lisa. Determine as forças internas no ponto J em termos de P , r e .
Passo 1
Alô Alô, galerinha do responde ai, tudo bem?
Bora lá
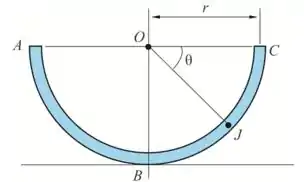
Dada meia seção do tubo
Passo 2
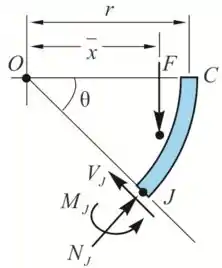
O diagrama de corpo livra da seção CJ é
Passo 3
O peso por unidade de comprimento do arco é W
O centro de gravidade de uma seção em ângulo é
A força total para baixo em J é o peso da seção , logo
A componente da força cortante no ponto J é
A componente normal da força no ponto J é
O momento no ponto J é
Resposta
Vide o passo a passo.