Meia seção de um tubo, com peso P e comprimento unitário, repousa sobre uma superfície horizontal lisa. Determine as forças internas no ponto J em termos de P , r e .
Passo 1
Falaiii meus amores, cêis tão suave?
Bora pra mais uma??
Então, encostaa!!
Vamos considerar o diagrama de corpo livre da figura inteira
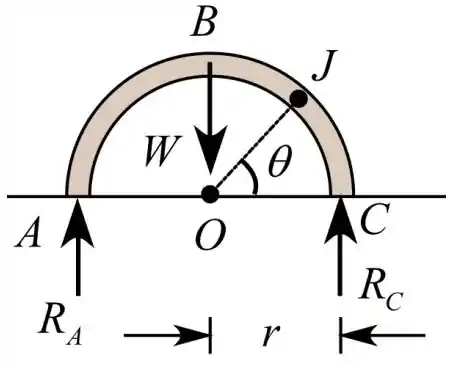
Considerando o equilíbrio de momentos em C, para calcular a reação em A
Onde, a reação em A é , o peso do tubo de meia seção é W e o raio do tubo é r.
Passo 2
Considerando uma seção no ponto J e desenhando o D.C.L do lado esquerdo da seção do tubo.
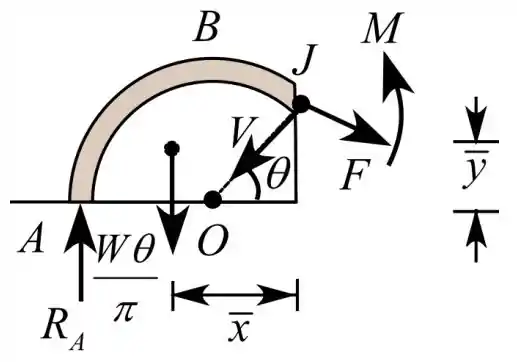
Calculando a distância centroidal do sistema, ao longo do eixo x, usando a fórmula
Considerando o equilíbrio de forças verticais, para calcular a reação vertical no ponto J
Passo 3
Considere o equilíbrio de forças horizontais, para calcular a reação horizontal no ponto J
Substituindo a 1 na 2, temos
Portanto, a reação vertical em J é
Substituindo por V na expressão 2, temos
Portanto, a reação horizontal em J é
Vamos considerar o equilíbrio de momentos em J, para calcular o momento fletor no ponto J
Portanto o momento em J é
Resposta
Vide o passo a passo.