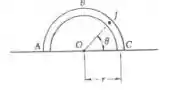
Meia seção de um tubo repousa sobre uma superfície horizontal sem atrito, como ilustrado. Se a massa da seção é de 12 kg e o diâmetro é de 400 mm, determine o momento fletor no ponto J quando .
Passo 1
Boraaa galerinha, aniimaaa, vamos resolver mais um!!
Só bora então!!
O nosso diagrama de corpo livre fica da seguinte maneira
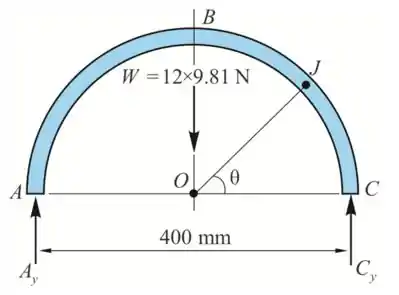
Tomemos momentos sobre o ponto A
Passo 2
Diagrama de corpo livre do setor CJ quando .
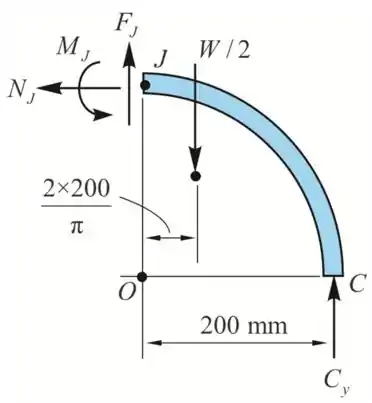
Das equações de equilíbrio ao longo do eixo x, temos
Portanto, a força normal que atua no ponto J é .
Passo 3
Das equações de equilíbrio ao longo do eixo y
Portanto, a força cortante que atua no ponto J é .
Tomemos momentos sobre J
Portanto, o momento fletor no ponto J é .
Resposta
Portanto, a força normal que atua no ponto J é .
Portanto, a força cortante que atua no ponto J é .
Portanto, o momento fletor no ponto J é .