Uma mola sem massa de comprimento b e constante elástica k conecta duas partículas de massas e O sistema repousa em uma mesa lisa e pode oscilar e girar.
- Determine as equações de movimento de Lagrange.
- Quais são as quantidades de movimento generalizadas associadas com quaisquer coordenadas cíclicas?
- Determine as equações de movimento de Hamilton
Passo 1
Faaaaaala, galera... Tranquileba??
Para a)
Fazendo um esboço da situação dita no enunciado, temos:
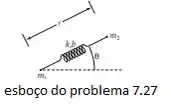
Usando as coordenadas polares e :
Assim obtemos a lagrangiana:
A equação de movimento para é:
Assim é constante
E para
E igualmente, é constante
Para
E finalmente, para :
E assim temos todas as equações de movimento.
Bora pro próximo passo?!
Passo 2
Obrigado por vir.
Para b)
Como dizemos no item a)
Logo, a quantidade é inalterado.
Passo 3
Para c)
Redizendo a)
Assim:
Assim, tomando que essas coordenadas não dependem do tempo, a energia total é hamiltoniana:
E as equações de movimento dos momentos canônicos são:
Resposta
Para a)
Para b)
Para c)