Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 10.Problemas - Ex. 23
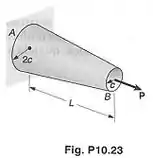
Mostrar por integração que a energia de deformação da barra , em forma de tronco de cone, é:
onde é a área de seção transversal na extremidade .
Passo 1
Oie, galerinha! Tudo certinho? Então bora fazer um exercício sobre energia de deformação!
Nesse problema o enunciado pede que a gente mostre como chegar na fórmula de energia de deformação de um tronco de cone!
Mas qual é a grande diferença entre calcular de um tronco e de uma barra comum?
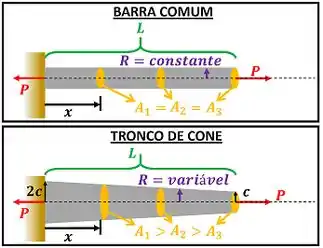
A diferença, como vemos pela figura acima é que a área de seção transversal varia em um cone. Em uma barra normal ela não varia.
Mas quais os efeitos que isso tem sobre os cálculos que precisamos fazer para achar ?!
Para entender melhor, precisamos olhar para a integral que usamos para calcular .
é a força axial que traciona a barra, é o módulo de elasticidade, é o comprimento da barra e é a distância axial da parede onde a barra está fixa até um ponto da barra.
Como a área do tronco não é constante, não podemos tirar da integral. Isso significa que para integrar, vamos precisar achar uma equação para em função de .
Como achar uma equação para o é fundamental para resolver essa integral, isso será a primeira cosia que devemos fazer. Depois de achar essa equação de , nós vamos resolver a integral pelo método de substituição simples. Por fim, a gente deve calcular quanto vale a área mínima do tronco e substituir o resultado na equação de .
Passo 2
Nesse passo nós vamos achar uma equação da área em função de . Contudo, sabemos que a fórmula de uma área circular como a de um cone depende do raio . é igual a:
Por conta disso, para achar uma fórmula de em função de , temos que achar primeiro uma fórmula de em função de !
A figura abaixo mostra que varia de forma linear com . Ou seja, a equação de em função de é a equação de uma reta do tipo , onde é o raio!
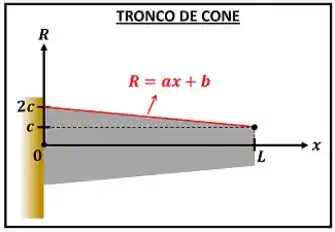
é a inclinação da reta. Ou seja, ela é medida, calculando .
é o ponto onde a reta corta o eixo . Ou seja, é igual a:
Substituindo isso na equação da reta , achamos:
Substituindo essa equação de na equação de , achamos:
Pronto, achamos . Agora vamos substituir na integral para achar !
Passo 3
Nesse passo a gente vai achar , resolvendo a integral pelo método de substituição simples!
Então sem enrolação! Vamos substituir a equação de que encontramos na integral.
Vamos colocar todas as constantes para fora da integral, porque elas não interferem na integração.
Agora vamos substituir por e por .
Resolvendo a integral e fazendo virar de novo, achamos:
Organizando a equação de , achamos:
Passo 4
Enfim estamos prontos para cumprir a última etapa da demonstração que é dividir pela área mínima !
Mas quanto vale a área mínima ?
O raio dessa área vale . Logo:
está no denominador de . Substituindo esse por , achamos:
Aeeee! Mostramos como se chega nessa fórmula. Demorou, mas conseguimos!
Resposta
Ei, a resposta está no passo a passo :)