Mostre que a expressão relativística para a energia cinética de uma partícula espalhada através de um ângulo por uma partícula alvo de igual massa é:
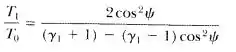
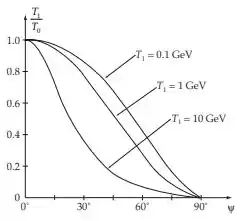
A expressão, evidentemente, se reduz à Equação 9.89a no limite não relativístico . um esboço para o espalhamento de nêutron-próton para as energias de nêutron dentes de 100 MeV, 1 GeV e 10GeV.
Passo 1
Fala galera, beleza? Nessa nós queremos calcular:
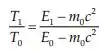
Onde T e E representam a energia cinética e total no sistema de laboratório, respectivamente, os subscritos 0 e 1 indicam os estados inicial e final, e é a massa de repouso da partícula incidente.
Assim a expressão para em termos de é:
![]()
Passo 2
pode ser relacionado com , energia total da partícula 1 no centro do referencial de momento após a colisão, através da transformação de Lorentz [cf. Eq. (14.92)] (lembrando que para a transformação inversa, trocamos as variáveis com e sem primer e mudamos o sinal de .
![]()
Onde:
![]()
![]()
![]()
E então:
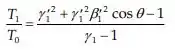
Passo 3
Para o caso de colisão entre duas partículas de igual massa, temos:
![]()
E consequentemente:
![]()
Assim:
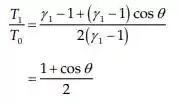
Passo 4
Devemos agora relacionar o ângulo de espalhamento no centro do sistema de quantidade de movimento com o ângulo dentro o sistema estudado.
Resolvendo para e termos de , temos:
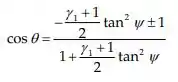
Uma das raízes da equação acima corresponde a , ou seja, a partícula incidente inverte sua trajetória e é projetada de volta ao longo da direção incidente. Substituindo a outra raiz:
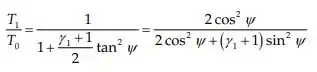
Vamos manipular o denominador:
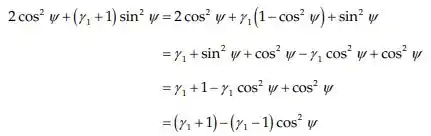
Resposta
E... e... RECEBAA! Chegamos no resultado esperado:
![]()
Note ainda que a forma da curva muda quando e .