O movimento de um par de osciladores acoplados pode ser descrito pelo uso de um método similar ao utilizado na construção de um diagrama de fase para um oscilador simples (Seção 3.4). Para osciladores acoplados, as duas posições x1(t) e x2(t) podem ser representadas por um ponto (o ponto do sistema) no espaço de configuração de duas dimensões x1 – x2. Conforme t aumenta, o local de todos estes pontos define uma certa curva. Os locais da projeção dos pontos do sistema nos eixos x1 e x2 representam os movimentos de m1 e m2, respectivamente. No caso geral, x1(t) e x2(t) são funções complicadas e, portanto, a curva também é complicada. Mas é sempre possível rotacionar os eixos x1-x2 para um novo conjunto x1’ – x2’ de tal forma que a projeção do ponto do sistema em cada um dos novos eixos seja harmônica simples. Os movimentos projetados ao longo dos novos eixos acontecem com as frequências características e correspondem aos modos normais do sistema. Os novos eixos são chamados de eixos normais. Encontre os eixos normais para o problema discutido na Seção 12.2 e verifique as afirmações anteriores em relação ao movimento relativo a este sistema coordenado.
Passo 1
E aí pessoal, belezinha? Vamos trabalhar agora em algumas questões de oscilações acopladas.
As soluções gerais para x1(t) e x2(t) são dadas pelas Eqs. (12.10). Para as condições iniciais, escolhemos o oscilador 1 para ser deslocado a uma distância D de sua posição de equilíbrio, enquanto o oscilador 2 é mantido em x2 = 0, e ambos são liberados do repouso:
Substituindo nas equações 12.10 temos que:
Onde:
Como exemplo, tome ω1 = 1,2ω2; x1(t) vs. x2(t) é plotado abaixo para este caso.
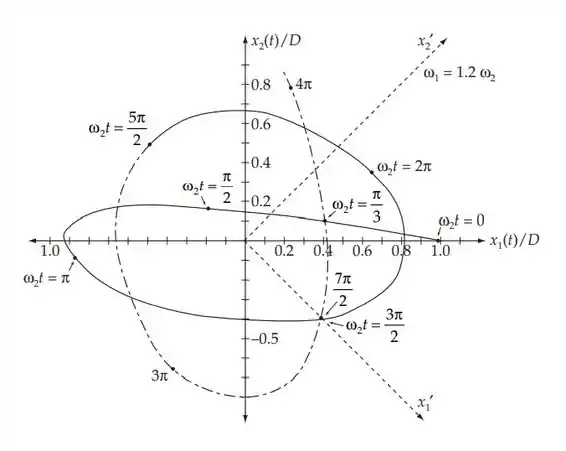
É possível encontrar uma rotação no espaço de configuração tal que a projeção do ponto do sistema em cada um dos novos eixos seja harmônica simples.
Por inspeção das equações, as novas coordenadas devem ser:
Esses novos eixos normais correspondem à descrição dos modos normais. Eles são representados por linhas tracejadas no gráfico da figura.
Resposta
Ver passo a passo.