Um novo foguete de um estágio é desenvolvido em 2023 com uma velocidade de exaustão de 4.000 m/s. A massa total do foguete é 105 kg, com 90% de sua massa sendo constituída por combustível. O combustível é queimado rapidamente durante 100 s em taxa constante. Para fins de testes, o foguete é lançado verticalmente a partir do repouso na superfície da Terra. Responda os itens (a) a (d) do problema anterior.
Passo 1
E aí pessoal, belezinha? Vamos trabalhar agora em algumas questões de dinâmica de um sistema de partículas.
Começamos com a equação do movimento de um foguete influenciado por uma força externa, Eq. (9.160), incluindo a gravidade e, posteriormente, a resistência do ar.
Item a
Há apenas aceleração constante devido à gravidade para se preocupar, então o problema pode ser resolvido analiticamente. Da Eq. (9.166), podemos obter a altura do foguete no esgotamento:
Onde mb é a massa do foguete na queima e α = (m0 – mb) tb. A substituição dos valores dados dá . Após a queima, o foguete percorre um adicional de , onde vb é a velocidade do foguete na queima. A altura final do foguete acaba sendo , depois de tudo levado em conta.
Passo 2
Item b
A situação e, portanto, a equação diferencial, torna-se mais complicada quando a resistência do ar é adicionada. Substituindo:
Na Equação (9.160), obtemos:
Devemos lembrar que a massa m também é função do tempo e, portanto, devemos incluí-la também no sistema de equações. Para ser específico, o sistema de equações que devemos usar para fazer isso por computador são:
Estes devem ser integrados desde o início até o tempo de esgotamento e, portanto, devem ser integrados com a substituição α = 0. Em primeiro lugar, obtemos que a velocidade e a altura no esgotamento são:
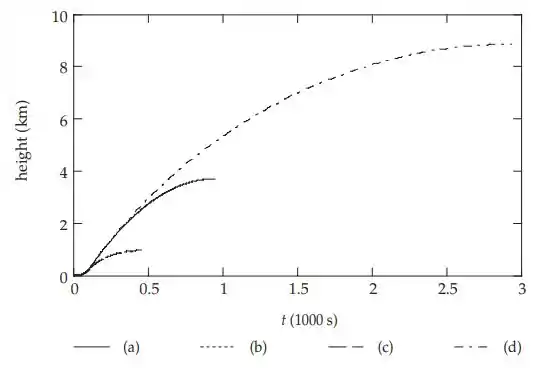
Podemos integrar numericamente para obter a segunda parte da jornada, ou usar os resultados do Problema 9-63(b) para nos ajudar a obter a distância adicional percorrida com a resistência do ar, analiticamente. A altura total até a qual o foguete sobe é de 890 km em um tempo total de vôo de 410 s.
Passo 3
Item c
A variação na aceleração da gravidade é levada em conta substituindo:
Isto nos dá:
com altura total de 950 km e tempo de vôo de 460 s.
Passo 4
Item d
Agora, basta substituir a expressão dada para a densidade do ar ρ(y) para ρ, na equação diferencial da parte (c). Isto dá:
e altura total de 8.900 km com tempo de voo de 2.900 s.
Resposta
Ver passo a passo.