Um novo lançador de projéteis é desenvolvido em 2023, capaz de lançar um projétil esférico de 104 kg com velocidade inicial de 6000 m/s. Para fins de teste, os objetos são lançados verticalmente.
- Despreze a resistência do ar e suponha que a aceleração da gravidade é constante. Determine altura que pode ser alcançada pelo objeto Iançado acima da superfície da Terra.
- Se o objeto tiver um raio de 20 cm e a resistência do ar for proporcional ao quadrado da velocidade do objeto com cw = 0,2, determine a altura máxima alcançada. Suponha que a densidade do ar é constante.
- Inclua agora o fato de que a aceleração da gravidade decresce à medida que o objeto sobrevoa a Terra. Determine a altura alcançada.
- Acrescente os efeitos do decréscimo da densidade do ar com a altitude no cálculo. Podemos representar de forma aproximada a densidade do ar por log10(ρ) = –0,05h + 0,11, onde ρ é a densidade do ar em kg/m3 e h é a altitude acima da Terra em km. Determine a altura agora alcançada pelo objeto.
Passo 1
E aí pessoal, belezinha? Vamos trabalhar agora em algumas questões de dinâmica de um sistema de partículas.
Item a
Sem resistência do ar e gravidade constante, o problema é simples:
Dando a altura máxima do objeto como:
O tempo que leva para fazer isso é:
Passo 2
Item b
Quando adicionamos a expressão para a resistência do ar, a equação diferencial que descreve a subida do projétil é:
Onde a velocidade terminal é:
Usando 1,3 kg/m3 como a densidade do ar, teremos que a solução desta equação diferencial dá:
Que nos dá v = 0 no tempo . A velocidade pode, por sua vez, ser integrada para fornecer a coordenada y do projétil na subida. A altura que atinge é a coordenada y no tempo τ:
Passo 3
Item c
Mudando a aceleração da gravidade de:
Muda nossa equação diferencial para y para:
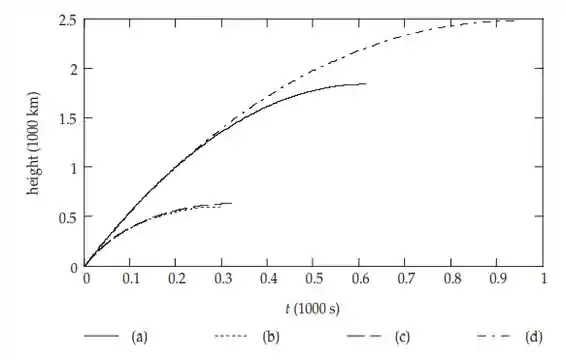
Usando as técnicas numéricas usuais, descobrimos que o projétil atinge uma altura de 630 km em um tempo de vôo de 330 s.
Passo 4
Item d
Agora devemos substituir o ρ na equação de resistência do ar por ρ(y). Dada a dependência de ρ, podemos escrever a equação diferencial:
Onde usamos:
O projétil atinge então uma altura de 2500 km em um tempo de vôo de 940 s.
Resposta
Ver passo a passo.