Obtenha, diretamente por integração, as expressões para e dadas na Fig 5.8 para:
43. Superfície sob uma parábola de grau .
Passo 1
Falaaa.. belezinha???
Nessa questão vamos usar as equações para centróide:
E já vamos começar fazendo o desenho da figura e separando um elemento infinitesimal:
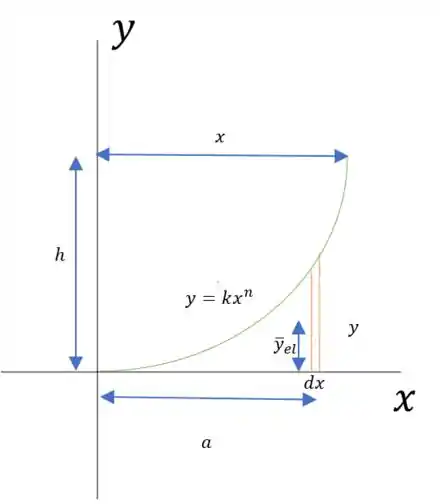
E nessa questão nós já sabemos o que temos que achar no final... Só olhar na tal figura 5.8, que é uma tabela:
Passo 2
Vamos primeiro achar a área da figura:
Temos a equação da curva:
E se liga só que podemos achar o valor de ..
Para temos , então:
Agora precisamos definir quem é o bendito .
Repara só que a gente pegou um elemento beeeemmmm fininho, de largura , então podemos considerar esse elemento como um retângulo de largura e altura .
Daí então temos que:
E aí sim podemos calcular a área:
E para a posição do centróide do elemento:
Passo 3
Agora sim é só partir pro abraço e usar as equações.
Para :
Passo 4
Para :
Ufa... essa deu um trabalhinho, mas foi. =)