Obtenha a resposta de um oscilador linear para uma função degrau e uma função de impulso (no limite ) para sobreamortecimento. Desenhe as funções resposta.
Passo 1
E aí galera, tudo beleza? Primeiro vamos ver a resposta para a função degrau.
é definido como:
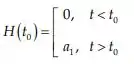
Com as condições iniciais e , a solução geral será dada por:
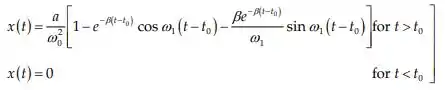
Onde
![]()
Para o caso de sobreamortecimento e consequentemente é um número puramente imaginário. Por isso, e não são mais funções oscilatórias, ao invés disso são transformadas em funções hiperbólicas. Portanto , perceba que é puramente real:
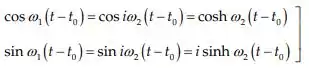
E a resposta será dada por:
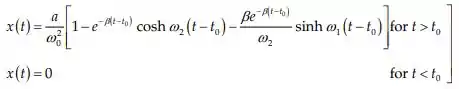
E agora para ajudar nossos neurônios, e simplificar a equação, vamos escolher , e a solução se torna.
![]()
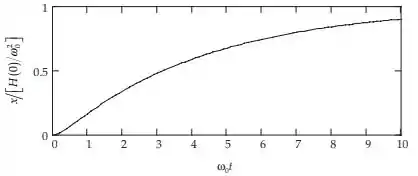
Passo 2
E agora galerinha do bem vamos analisar a resposta para uma função impulso no limite , vamos lá sigam-me os bons.
Uma função impulso é definida como:
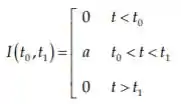
Para de forma que , a resposta da função será dada por:
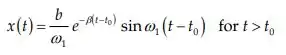
Novamente vamos simplificar adotando , temos:
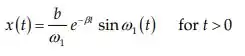
Para a solução será:
![]()
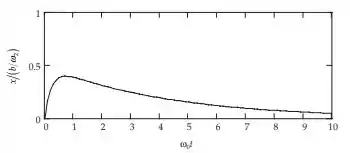
Resposta
Ei, a resposta está no passo a passo :)