Faala meu povo, bora com tudo pra mais uma questão do nosso livro!
Primeiramente temos que a equação para um oscilador linear acionado é:
onde é a senóide mostrada no diagrama abaixo.
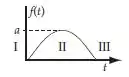
A solução para a região 2 é dada por:
No qual:
Onde:
Assim,
A condição inicial nos dá:
E ,
Ou
A solução da região (3) é dada:
Nós exigimos que e para as regiões (2) e (3) coincidem em . A condição que: então:
Onde: ou,
A condição que então:
Ou
Ou
Substituindo em (4) de (3), temos:
Do qual:
Usando (3), podemos encontrar :
Substituindo , e de (2), (1) e (5), temos:
Assim, obtivemos todas as constantes nos dando as funções de resposta explicitamente.
E assim finalizamos nossa questão.
