Um oscilador linear amortecido, originalmente no repouso em sua posição de equilíbrio, está sujeito a uma função de força conforme:
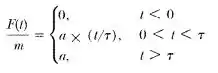
Determine a função resposta. Considere e demonstre que a solução se torna aquela de uma função degrau.
Passo 1
E aí galera, tudo beleza? Nessa questão vamos iniciar reescrevendo a função da força, que consiste em duas funções de força baseadas em :
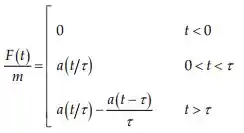
Durante o intervalo , a equação diferencial que descreve o movimento é:
![]()
A solução particular é , e substituindo na equação anterior:
![]()
De onde:
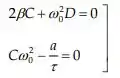
Portanto:
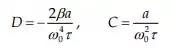
Que nos dá:
![]()
Assim a solução geral para é:
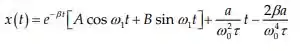
Então:
![]()
Passo 2
Êeeee calculera.... segue o jogo...
As condições iniciais , impõem que:
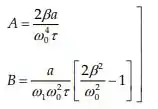
Portanto a função resposta é:
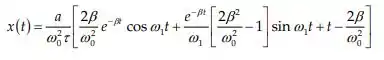
Para a função da força do passo 1, temos uma resposta similar na equação anterior, e daí adicionamos essas duas equações para obter a função resposta total:
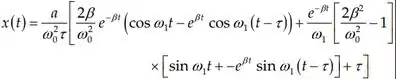
Quando podemos aproximar até , e ainda , . Então:
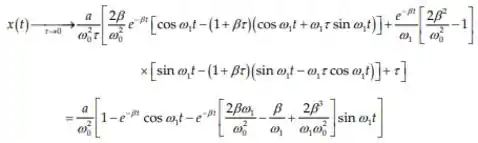
Resposta
Se usarmos o coeficiente de se torna . Portanto:
![]()
Olha só que maneiro, isso é a resposta de uma função degrau.