A parte superior de uma lata é removida e a lata vazia é invertida sobre um par de bolas de bilhar sobre uma mesa, conforme mostrado no desenho. Para certas combinações de tamanhos e pesos, a configuração mostrada é estável. Para outras combinações, a lata tomba quando liberada. É proposto montar uma demonstração para uma palestra sobre temperança usando em sequência uma lata de suco de laranja congelado e uma lata de cerveja com o mesmo par de bolas de bilhar. Investigue se o tombamento ocorrerá para os seguintes tamanhos e pesos.
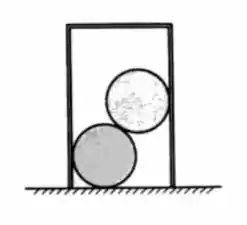
Passo 1
O procedimento é assumir a estabilidade e então ver se as forças necessárias podem sair.
Suposições: Atrito de Lero nas superfícies das esferas; atrito infinito entre a mesa e a lata.
Corpo livre das bolas juntas
Geometria:
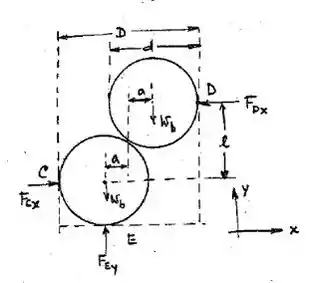
Equilíbrio
Ou
Passo 2
Corpo livre da lata: Suponha o equilíbrio possível. A força na reação da mesa, a alguns radinos x do eixo.
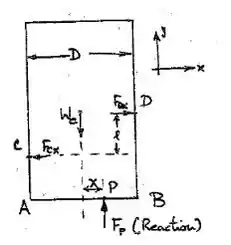
Equilíbrio
Essas duas equações
Para
Equilíbrio possível
Para a lata de cerveja
Equilíbrio não possível