Um pêndulo duplo consiste de dois pêndulos simples, com um pêndulo suspenso do peso clo outro. Se dois pêndulos tiverem comprimentos iguais e pesos de massa igual, e se ambos estiverem com movimentos restritos no mesmo plano, encontre as equações de movimento de Lagrange para o sistema. Náo pressuponha ângulos pequenos.
Passo 1
Faaaaaala, galera... Tranquileba??
Tiremos as sandálias de nossos pés, porque vamos ver a beleza do método Lagrangiano em ação.
Primeiro, vamos visualizar o dito:
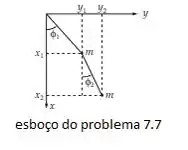
As coordenadas para o primeiro pendulo, como já sabemos é:
E para o segundo, o qual depende do primeiro:
Sendo r o comprimento do fio.
E escrevendo a função Lagrangiana, temos:
Vamos assumir a coordenadas generalizadas cartesianas, de forma a facilitar. Assim:
Bora pro próximo passo?!
Passo 2
Obrigado por vir.
Agora vamos substituir.
Temos:
E para U:
Assim:
+
Passo 3
Assim a equação matricial para lagrange temos:
Onde:
Assim a equação matricial fica: