um pêndulo esférico consiste de um peso de massa m conectado a uma barra sem peso, sem extensão, de comprimento l. A extremidade da barra oposta ao peso faz o pivô livremente (em todas as direções) sobre algum ponto fixo. Estabeleça a função hamiltoniana em coordenadas esféricas. (Se o resultado é o mesmo que o do pêndulo plano.) Combine o termo que deperde de com o termo de energia potencial comum para definir como potencial efetivo Represente v como uma função de para valores diversos de , incluindo . . Discuta as características do movimento, apontando as diferenças entre e . Discuta o caso limite do pêndulo cônico ( constante) em relação ao diagrama .
Passo 1
Faaaaaala, galera... Tranquileba??
Fazendo um esboço da situação dita no enunciado, temos:
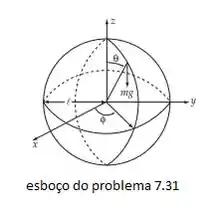
Não se esqueça de que há a energia cinética de rotação, e nõ nos diz se há a esfera está rolando, logo é somente a energia cinética de rotação. Façamos a energia cinética do pendulo esférico:
E a energia potencial é:
Assim a lagrangiana é:
Bora pro próximo passo?!
Passo 2
Obrigado por vir.
Escrevamos os momentos canônicos, então:
Assim a hamiltoniana é:
Onde :
Passo 3
Veja que para é finito e máximo quando , que é o topo da esfera, e minim quando , parte inferior da esfera. Para valores diferentes de , o gráfico de tem a seguinte aparência.
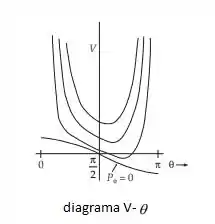
Quando o pendulo nunca alcança ou por causa da dependência de seno na primeira parte, por isto V é finito nesse pontos
Resposta
E a discussão se encontra no passo 3 da resolução.