Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Gere, Mecânica dos Materiais- Ed: 5º - Capítulo 5.5 - Ex. 12

Uma pequena barragem de altura h = 2,4   m é construída de vigas de madeiras verticais AB de espessura b = 150   m m , conforme ilustrado na figura. Considere que as vigas são apoiadas de forma simples no topo e na base. Determine a tensão fletora máxima σ m á x nas vigas , assumindo que o peso específico da água é γ = 9,81   k N / m 3 .

Passo 1

Hellooooooou It’s meeeee, bora pra mais umaaaaa?

Primeiro passo e desenhar o nosso D.C.L, porém vou adotar a espessura sendo como t no meu diagrama

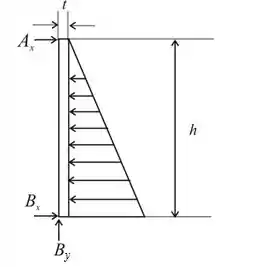
Passo 2

Agora iremos redesenhar esse D.C.L na horizontal

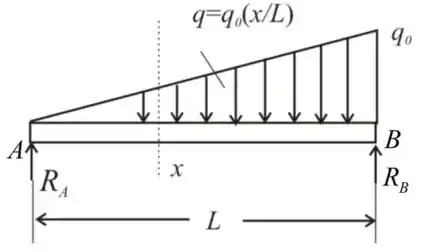
Para um triângulo, a carga total atua exatamente a uma distância 2 L 3 do ponto A e L 3

Do ponto B.

Passo 3

Consideremos a soma algébrica de momentos sobre o ponto B em zero.

∑ M B = 0

R A L - 1 2 q 0 L L 3 = 0

R A = 1 6 q 0 L

Passo 4

Vamos desenhar o diagrama de corpo livre da seção

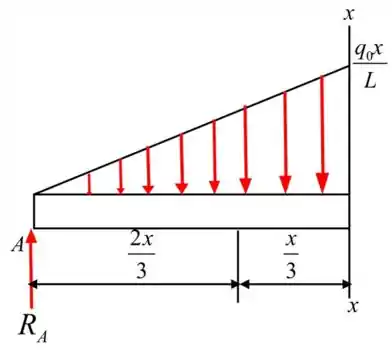
Passo 5

Considerando a soma algébrica de momentos sobre a seção x - x sendo zero

M x = R A x - 1 2 × q 0 x L × x × x 3

M x = R A x - q 0 x 3 6 L

Substituindo

1 6 q 0 L       p o r     R A

M x = 1 6 q 0 L   - q 0 x 3 6 L                                 ( 1 )

Passo 6

Iremos calcular a localização do momento fletor máximo da seguinte maneira:

d M d x = 0

d 1 6 q 0 L x - q 0 x 3 6 L d x = 0

1 6 q 0 L - 3 q 0 x 2 6 L = 0

L - 3 x 2 L = 0  

x 2 = L 2 3

x = L 3

Passo 7

Calcularemos o momento de flexão máximo da seguinte maneira:

Substituindo L 3 por x na equação (1)

M m á x = q 0 L x 6 - q 0 x 3 6 L

M m á x = q 0 L L 3 6 - q 0 L 3 3 6 L

M m á x = q 0 L 2 6 3 - q 0 L 2 18 3

M m á x = 2 q 0 L 2 18 3

M m á x = q 0 L 2 9 3

Para vigas de madeiras verticais, o comprimento da viga de madeira é igual á altura da barragem.

L = h

M m á x = q 0 h 2 9 3

Passo 8

Escreveremos a relação para o módulo de seção da viga

S = b t 2 6

Para o calculo da tensão de flexão máxima na viga

σ m á x = M m á x S

Pela dedução no passo anterior, iremos substituis os resultados nesse novo passo

σ m á x = q 0 h 2 9 3 b t 2 6

σ m á x = 2 q 0 h 2 3 3 b t 2

Passo 9

Nesse passo iremos fazer mais algumas alterações nas expressões

Como a substituição de γ b h por q 0

σ m á x = 2 ( γ b h ) h 2 3 3 b t 2

σ m á x = 2 ( γ ) h 3 3 3 t 2

Passo 10

Para finalizar este exercício vamos fazer as devidas substituições

σ m á x = 2 9.81 2.4 3 3 3 0.15 2

σ m á x = 2319.895   k P a

σ m á x = 2.32   M P a

Resposta

Portanto, a tensão máxima de flexão é de 2.32 Mpa.