Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Gere, Mecânica dos Materiais- Ed: 5º - Capítulo 5.5 - Ex. 23

Uma pequena barragem de altura h =   6 f t é construída de vigas de madeira vertical AB, conforme ilustrado na figura. As vigas de madeira, que têm espessura t = 2,5   i n , estão simplesmente apoiadas em vigas de aço horizontais nos pontos A e B.

Construa um gráfico mostrando as tensões fletoras máximas σ m á x mas vigas de madeira v e r s u s a profundidade d da água acima do apoio inferior em B. Trace a tensão σ m á x (psi) como ordenada e a profundidade d   (ft) como abscissa. (Nota : O peso específico γ da água é igual a 62,4   l b / f t 3 .)

Passo 1

Falaaa seres de luz, tudo na paz??

Só vamoo??

Simboraáaaa

Alguns dados fornecidos pelo enunciado:

Altura da barragem h = 6 f t .

Espessura da viga t = 2.5   i n .

Densidade de peso γ = 62.4   l b / f t 3 .

Presumi

Largura da viga b .

Intensidade de carga em d = q .

Onde q = γ b d

Passo 2

Viga da barragem

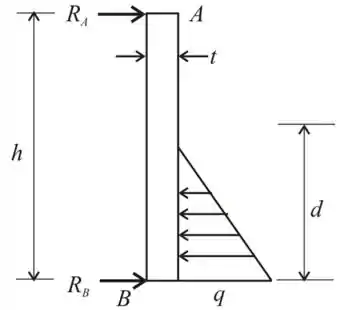
Passo 3

Por equilíbrio

R A + R B = q d 2                                   ( 1 )

Tomaremos momento em B

- R A h + 1 3 q d 2   d = 0

R A = q d 2 6 h

Pela expressão (1) substituindo

q d 2 6 h + R B = q d 2

R B = q 2 d - q d 2 6 h

R B = q d 6 3 - d h

Passo 4

O feixe assume a posição horizontal

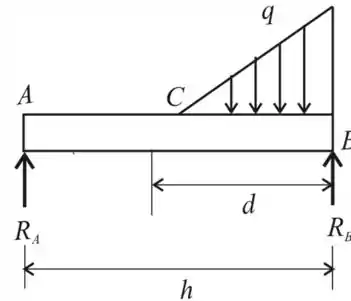
Passo 5

Seção entre A até C

Forma de cisalhamento   V A = R A

V A = q d 2 6 h

V C = q d 2 6 h

Força de cisalhamento em B   V B = R B

V B = q d 6 3 - d h

Momento de flexão máximo

M m á x = q d 2 6 1 - d h + 2 d 3 h d 3 h

Módulo máximo da seção

σ m á x = M m á x S

Quando o módulo de seção

S = 1 6 b t 2

Então

σ m á x = q d 2 6 1 - d h + 2 3 h d 3 h 1 6 b t 2

σ m á x = q d 2 b t 2 1 - d h + 2 d 3 h d 3 h

Onde temos que q = γ b d .

Passo 6

Então

σ m i n = γ b d d 2 b t 2 1 - d h + 2 d 3 h d 3 h

σ m i n = γ d 3 t 2 1 - d h + 2 d 3 h d 3 h

σ m i n = 62.4 d 3 2.5 2 1 - d 6 + 2 d 3 × 6 d 3 × 6

σ m i n = 9.984 d 3 1 - d 6 + d 9 d 18

Passo 7

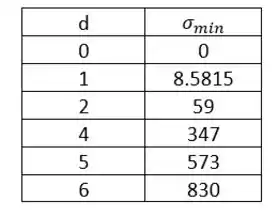
Passo 8

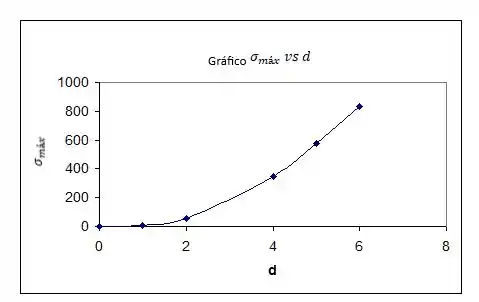
Resposta

Então, em d = 6 f t

σ m á x = 830   p s i