Uma ponte flutuante (veja a figura) é construída de duas vigas de madeira longitudinais, conhecidas como madeiros, que formam vão entre flutuadores adjacentes e suportam o piso transversal de vigas, que são chamadas de pranchas de uma ponte de barcas. Para o propósito de projeto, vamos assumir que a carga uniformemente do piso de 10kPa atue sobre as pranchas de uma ponte de barcas. (Isso inclui a permissividade para os pesos das pranchas de uma ponte de barcas e dos madeiros).Além disso, assuma que as pranchas de uma ponte de barcas têm comprimento de 2,4 m e os madeiros estão simplesmente apoiados com um vão de 3,6 m. A tensão permitida na madeira é 17,5 MPa.
Se os madeiros têm uma seção transversal quadrada, qual é a largura mínima exigida?
Passo 1
Falaaaaaaaaaaaaa meus queridx’s , tudo na boaaa??
Pirmeiro passo e desenhar o diagrama de corpo livre da nossa viga
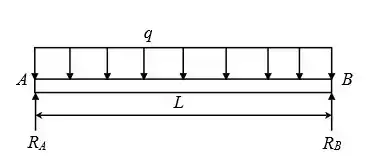
Passo 2
Determinaremos a carga de intensidade que atua em cada bloco de madeira
Substituindo
por
Substituindo os dados fornecidos pelo enunciado
Passo 3
Determinaremos o momento fletor máximo na viga de madeira
Substituindo valores
Passo 4
Determinaremos o módulo seccional da viga
Substituindo os devidos valores
Passo 5
Qual é a largura mínima exigida da viga de madeira se os empecilhos têm seção transversal quadrada
Substituindo os valores
Resposta
Portanto, a largura mínima exigida da viga de madeira se os empecilhos com seção transversal quadrada são de 188 mm.