Uma porta é fabricada com uma fina chapa homogênea de material: ela tem largura de 1m. Se a porta é aberta em ângulo de 90°, constata-se que, ao ser liberada, ela fecha sozinha em 2s. Suponha que as dobradiças não tenham atrito e demonstre que a linha de dobradiças deverá fazer um ângulo de aproximadamente 3° com a direção vertical.
Passo 1
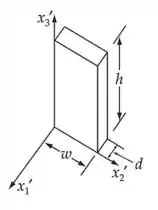
Deixamos ser o eixo vertical no sistema fixo. Este seria o eixo (ou seja, a linha de dobradiça) da porta se estivesse devidamente pendurada (sem autorrotação), conforme indicada no diagrama. A massa da porta é .
O momento de inércia da porta em torno do eixo é:
Lembrando que a porta é considerada como uma chapa fina,
Passo 2
A posição inicial da porta que fecha sozinha pode ser expressa como uma transformação em duas etapas, começando com a posição na figura do Passo 1. A primeira rotação é em torno do
um ângulo e a segunda rotação é em torno do eixo através de um ângulo .
Os eixos são os eixos do sistema fixo e os são os eixos do sistema rotativos que estão presos à porta. Aqui, o ângulo de Euler é zero.
Uma vez que esta rotação é realizada no sentido horário e não no sentido anti-horário, a matriz de rotação que transforma os eixos fixos nos eixos rotativos com e , será:
Passo 3
O procedimento é encontrar o torque que atua na porta expresso no sistema de coordenadas fixo e então obter o componente , ou seja, o componente no sistema rotativo. Observe que quando a porta é liberada a partir do repouso em algum ângulo inicial , a rotação é no sentido de diminuir E assim podemos escrever:
Onde , desde que .
Passo 4
As coordenadas do centro de massa da porta são:
Agora nós vamos aplicar a transformada inversa para R, então temos:
Passo 5
E a força gravitacional atuando na porta é:
E assim o torque que atua na porta é:
Portanto,
Substituindo com a equação do Passo 3:
Passo 6
Resolvendo
Essa equação pode ser integrada multiplicando-a por
Onde a constante de integração é zero, pois quando . Portanto:
Devemos escolher o sinal negativo, pois quando . Integrando novamente para os limites de até :
Onde , assim com o apoio das Integrais de Funções Gama podemos reescrever a integral acima, como:
Pelas Funções Gama características temos que:
Portanto
Resposta
E assim podemos resolver o início do Passo 6 para :
Substituindo os valores de e , encontramos: