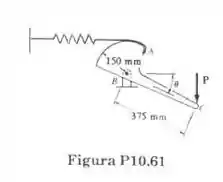
No Prob. 10.61, determine três valores de , correspondentes ao equilíbrio quando . Estabeleça em cada caso se o equilíbrio é estável, instável, ou indiferente.
Passo 1
Boraaa galerinha, aniimaaa, vamos resolver mais um!!
Só bora então!!
A figura mostra várias forças atuando na articulação
Passo 2
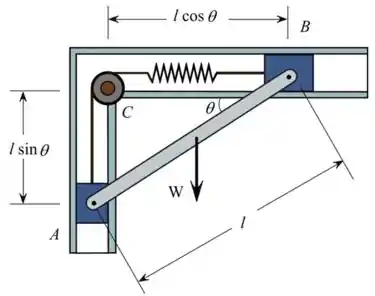
Considerando o eixo C e a coordenada do ponto são
Iremos encontrar o pequeno deslocamento vertical do bloco A
Da mesma forma, um pequeno deslocamento horizontal do bloco B
Encontraremos o deslocamento vertical do ponto D usando
O alongamento da mola é
Uma vez que a componente horizontal de A , C e a componente vertical de B não realizam nenhum trabalho . Pelo principio do trabalho virtual, a energia potencial é
Passo 3
Encontrando a primeira derivada da equação
Encontrando a segunda derivada
Para encontrar o substituto de equilíbrio,
Existe dois casos de resolução
E o segundo caso da solução é
Ou
Passo 4
Substituindo 90° por
Substituindo por
O sistema tem equilíbrio estável em
Substituindo por
O sistema tem equilíbrio instável em
Resposta
O sistema tem equilíbrio estável em
O sistema tem equilíbrio instável em