No problema anterior, se os eixos de coordenadas girarem por um ângulo em torno do eixo , demonstre que o novo tensor de inércia é:
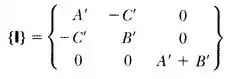
Onde
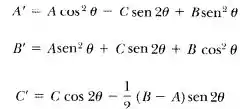
e, dessa forma, demonstre que os eixos se tornam os eixos principais se o ângulo de rotação é
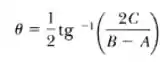
Passo 1
O novo tensor de inércia é obtido de por uma transformação de similaridade. Como nesse caso o foco é analisar apenas uma rotação em torno do eixo , a matriz transformada é apenas . Então:
Em que:
Passo 2
Portanto a matriz semelhante é:
Realizando as operações e simplificando, temos:
Fazendo as identificações estipuladas no problema, vemos que:
E:
Portanto:
Para que e sejam os eixos principais, é necessário que :
Também:
De onde podemos dizer:
Resposta
Ei, a resposta está no passo a passo :)