Prove que o momento polar de inércia em relação ao centroide de uma dada superfície A não pode ser menor que . (Sugestão : Compare o momento de inércia de um círculo de mesma área e mesmo centroide)
Passo 1
Alô Alô, galerinha do responde ai, tudo bem?
Bora lá
Vamos considerar um retângulo
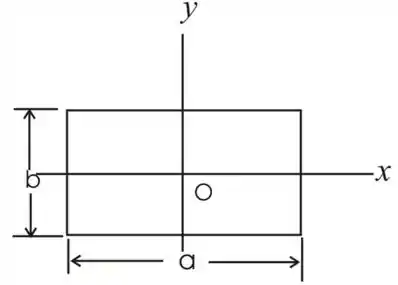
Passo 2
Temos
A área
Passo 3
Sendo assim
Comparando temos
Resposta
Portanto, o momento polar centroidal de inércia de uma dada área “A” não pode ser menor que .