A próxima figura mostra o esquema simplificado de um pórtico plano transversal de arquibancada de um estádio. Determine os diagramas dos esforços seccionais.
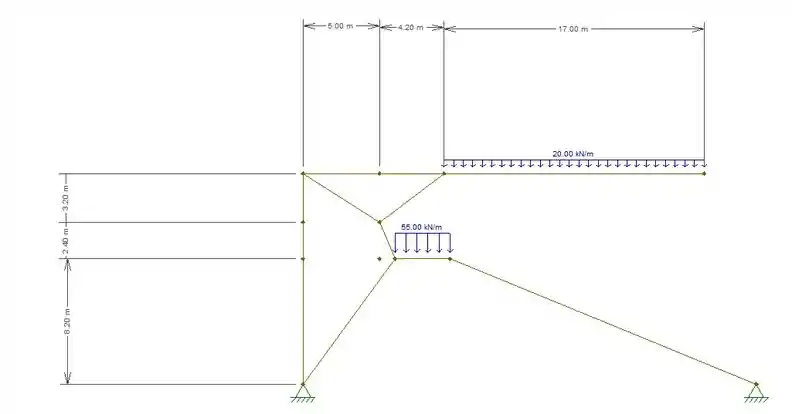
Passo 1
E aí.....tudo belezinha?
Para começarmos a calcular as reações normais por este método devemos escolher o melhor ponto para realizar o corte, lembrando que só pode-se cortar três barras e é melhor que mais de uma barra seja direcionado ao mesmo nó. Sendo assim, o melhor corte a ser realizado é o representando na imagem abaixo.
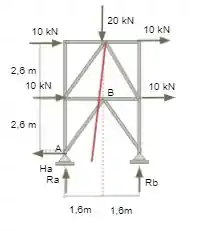
Passo 2
Agora podemos considerar as reações de apoio na estrutura, que pode ser interpretado como um sólido inteiriço, sendo assim as reações de apoio serão representadas como as encontradas na figura abaixo.
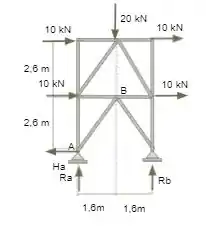
Para calcularmos as reações de apoio devemos levar em conta as reações de equilíbrio demonstradas logo abaixo.
Substituindo o valor de Rb encontrado na equação de momentos na equação encontrada no equilíbrio de forças horizontais, podemos encontrar o valor de Ra, como demonstrado abaixo:
Passo 3
Agora precisamos escolher um dos lados do corte da seção para realizar os cálculos, neste caso o lado que nos permite realizar o cálculo é o lado direito a figura, como podemos ver abaixo.
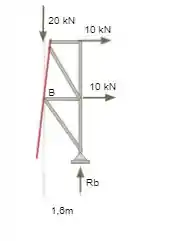
Agora precisamos realizar o equilíbrio da estrutura devolvendo as normais das barras que foram cortadas, como demonstrado abaixo.
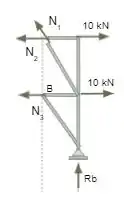
Neste caso devemos levar em conta que N1 e NAB possuem o mesmo valor numérico, porém orientações diferentes. Além disso vemos que N1 e N2 apontam para o mesmo nó, sendo assim podemos calcular o momento deste nó.
Agora devemos realizar o equilíbrio na vertical para descobrirmos o valor de N1=NAB ;
Para descobrirmos o ângulo podemos fazer a relação de altura comprimento da treliça, como representado abaixo.
Sendo assim, N1=NAB, será igual a:
E agora, bora para a próxima questão =)
Resposta
NAB=14,7kN;