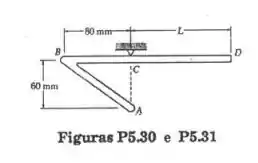
Com referência ao Prob. 5.30, determine o comprimento L para que a parte AB fique em posição horizontal.
Passo 1
E ai seres de luz, tudo bem?
Bora resolver mais uma?
Encostaaa!!
Já vamos dando inicio ao exercício fazendo o D.C.L do fio homogêneo
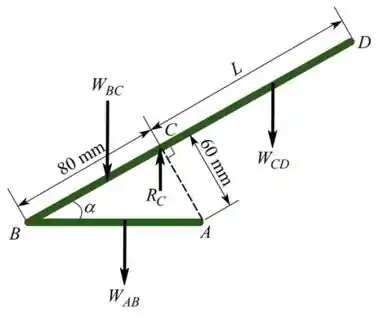
Passo 2
Vamos calcular o peso da seção BC
Calculando o peso da seção CD
Calculando o comprimento da seção AB usando o teorema de Pitágoras
Calculando o peso da seção AB
Passo 3
Vamos calcular o ângulo de inclinação do fio BCD com a horizontal
Vamos considerar a condição de equilíbrio de momentos em torno de C
Resposta
Portanto, o comprimento do fio entre as partes CD é de .