Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Gere, Mecânica dos Materiais- Ed: 5º - Capítulo 11.4 - Ex. 2

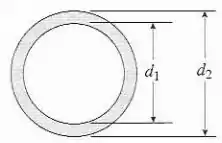
Resolva o problema anterior para uma coluna tubular de aço ( E = 210   G P a ) com comprimento L = 1500   m m , diâmetro interno d 1 = 36   m m e diâmetro externo d 2 = 40   m m .

Passo 1

Dados:

d 1 = 36   m m

d 2 = 40   m m

E = 210   G P a

L = 1500   m m

Bora lá galera!

Calculando o momento de inércia, temos que:

I = π 64 ⋅ d 2 4 - d 1 4 =   π 64 ⋅ 40 4 - 36 4

I = 43215,75   m m 4

Com isso my friends, basta aplicarmos nas fórmulas para cada ocasião.

(1) pino-pino

P c r = π 2 E I L 2

P c r = π 2 ⋅ 210 ⋅ 10 3 ⋅ 43215,75 1500 2

P c r = 39,81   k N

(2) livre-engastada

P c r = π 2 E I 4 L 2

P c r = π 2 ⋅ 210 ⋅ 10 3 ⋅ 43215,75 4 ⋅ 1500 2

P c r = 9,95   k N

(3) engastada-pino

P c r = 2,046 π 2 E I L 2

P c r = 2,046 ⋅ π 2 ⋅ 210 ⋅ 10 3 ⋅ 43215,75 1500 2

P c r = 81,45   k N

(4) engastada-engastada

P c r = 4 π 2 E I L 2

P c r = 4 ⋅ π 2 ⋅ 210 ⋅ 10 3 ⋅ 43215,75 1500 2

P c r = 159,23   k N

Essa questão foi, heim... Bora pra próxima?

Resposta

(1) pino-pino P c r = 39,81   k N

(2) livre-engastada P c r = 9,95   k N

(3) engastada-pino P c r = 81,45   k N

(4) engastada-engastada P c r = 159,23   k N