Enunciado
Mecânica e Resistência dos Materiais - Gere, Mecânica dos Materiais- Ed: 5º - Capítulo 7.2 - Ex. 8
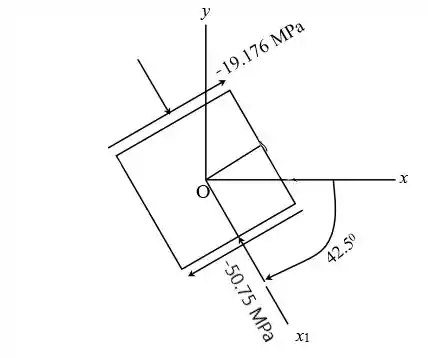
Resolva o problema anterior se as tensões normal e de cisalhamento agindo no elemento B forem 50 MPa , 8 MPa e 20 MPa (nas direções ilustradas na figura) e o ângulo for 42,5° (sentido horário).
Passo 1
Falaaa ai gente boa, bora?
Determinaremos a tensão normal atuando em face do elemento orientado em ângulo a partindo do , usando as equações de transformação da seguinte maneira:
Fazendo as devidas substituições
Portanto, a tensão normal atuando em face do elemento orientada em um ângulo de com eixo é de
Passo 2
Determinaremos a tensão de cisalhamento que atua no elemento orientado no ângulo do eixo x, usando as equações de transformação
Substituindo os devidos valores:
Portanto, a tensão de cisalhamento no plano inclinado é de .
Passo 3
Esboce a orientação do elemento e mostre as tensões atuando no elemento
