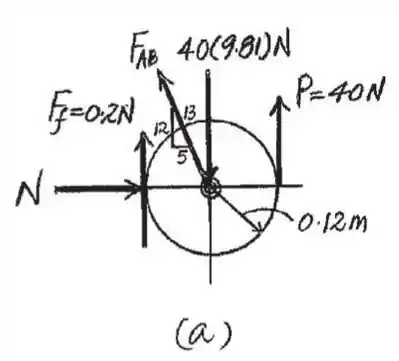
O rolo de papel de 40 kg repousa ao longo da parede onde o coeficiente de atrito cinético é . Se uma força vertical de P=40N for aplicada ao papel, determine a velocidade angular do rolo quando t=6 s partindo do repouso. Despreze a massa do papel desenrolado e considere o raio de giro do carretel em torno do eixo O como.
Passo 1
Princípio do Impulso e Momentum. O momento de inércia de massa do rolo de papel em torno de seu centro é. Como o rolo de papel deve deslizar no ponto de contato,. Referindo-se ao FBD do rolo de papel, Fig. a,
(1)
Passo 2
(2)
Passo 3
Resolvendo eq (1) e (2)
Subsequentemente