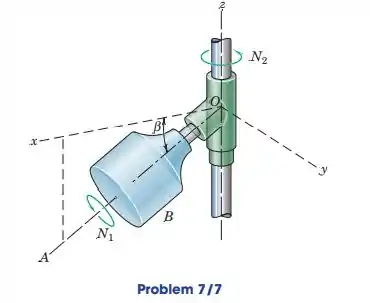
O rotor B gira em torno de seu eixo inclinado OA na velocidade , onde . Simultaneamente, o conjunto gira em torno do eixo z vertical em a taxa . Se a velocidade angular total do rotor tem uma magnitude de 40 rad/s, determine .
Passo 1
Falaiii meus amores, cêis tão suave?
Bora pra mais uma??
Então, encostaa!!
Vamos iniciar escrevendo o vetor unitário ao longo do eixo A
Calculando a velocidade angular ao longo do eixo A
Passo 2
Calculando o vetor ao longo do eixo A
Escrevendo a expressão para a velocidade angular total do rotor
Pegaremos a magnitude do vetor em RHS
Quadrado dos dois lados, temos
Passo 3
Resolvendo
Calculando a velocidade em
Resposta
Portanto, a velocidade .