Sabendo que cada roldana tem um raio de 100 mm, determine as forças internas nos pontos : (a) C e (b) J.
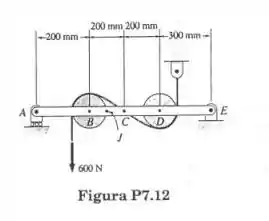
Passo 1
Boraaa galerinha, aniimaaa, vamos resolver mais um!!
Só bora então!!
Vamos começar com o D.C.L do membro AE
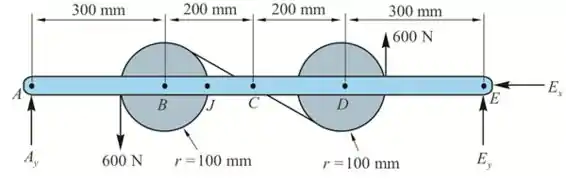
Tomemos momentos sobre E
Passo 2
- Consideremos a parte ABC:
- Consideremos a porção ABJ
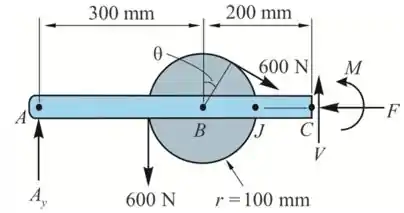
Da equação de equilíbrio ao longo do eixo x, temos
Portanto, a força normal em C na barra ABC é .
Da equação de equilíbrio ao longo do eixo y
Portanto, a força cortante em C na barra ABC é .
Tomemos momentos sobre C
Portanto, o momento fletor em C na barra ABC é .
Passo 3
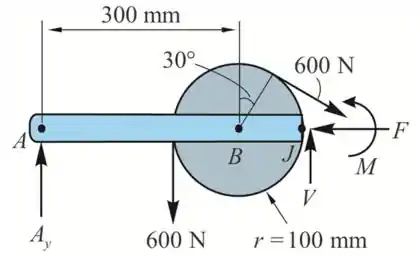
Da equação de equilíbrio ao longo do eixo x, temos
Portanto, a força normal em J na barra ABJ é .
Da equação de equilíbrio ao longo do eixo y
Portanto, a força cortante em J na barra ABJ é .
Tomemos momentos sobre C
Portanto, o momento fletor em J na barra ABJ é .
Resposta
- Portanto, a força normal em C na barra ABC é .
- Portanto, a força normal em J na barra ABJ é .
Portanto, a força cortante em C na barra ABC é .
Portanto, o momento fletor em C na barra ABC é .
Portanto, a força cortante em J na barra ABJ é .
Portanto, o momento fletor em J na barra ABJ é .