Sabenso que o objeto da figura é formado por um arame fino e homogêneo, determine o comprimento I da parte CE do fio de modo que o baricentro da figura fique localizado no ponto C, quando (a) e (b) .
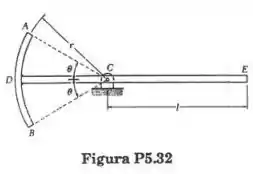
Passo 1
Falaiii meus amores, cêis tão suave?
Bora pra mais uma??
Então, encostaa!!
Vamos iniciar fazendo o D.C.L do fio
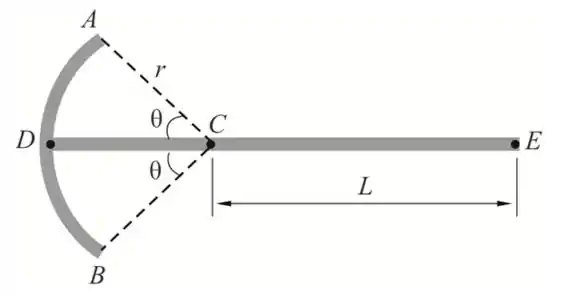
Passo 2
O centro de gravidade da figura está localizada no ponto C
As coordenadas do centroide de cada segmento de linha, calcularemos seus primeiros momentos em relação aos eixos coordenados
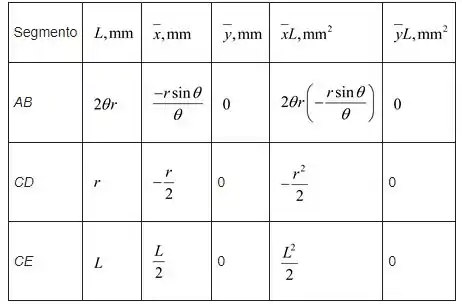
Passo 3
- Se
- Se
Portanto, o comprimento da porção .
Passo 4
Portanto, o comprimento da porção .
Resposta
- Portanto, o comprimento da porção .
- Portanto, o comprimento da porção .