A seção transversal da bitola estreita de uma ponte ferroviária é mostrada na parte (a) da figura. A ponte é construída com vigas mestras longitudinais que apoiam os dormentes de madeira. As vigas mestras são protegidas contra flambagem por reforço diagonal, conforme indicado pelas linhas tracejadas. O espaçamento das vigas mestras é e o espaçamento dos trilhos é . O carregamento transmitido de cada trilho para um dormente simples é . A seção transversal do dormente, mostrada na parte (b) da figura, tem largura e profundidade d.
Determine o valor mínimo de baseado em uma tensão fletora permitida de no dormente. (Desconsidere o peso próprio do dormente.)
Passo 1
E ai meus queridxx’ss vamos pra mais um??
Desenharemos o diagrama de corpo livre da seção transversal da ponte ferroviária.

Passo 2
Aplicaremos as equações de equilíbrio e calcularemos as reações verticais
Aplicaremos as equações de equilíbrio e calcularemos os momentos sobre o ponto .
Passo 3
Substituindo para na equação (1).
O diagrama de corpo livre representa a viga simplesmente apoiada com cargas simétricas.
Portanto, o momento fletor máxima será no centro da viga.
Desenharemos o D.C.L esquemático
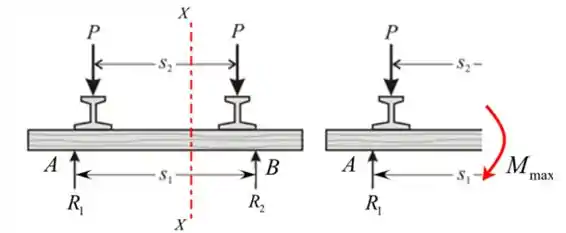
Passo 4
Aplicaremos as equações de equilíbrio e calcularemos o momento fletor máximo
Passo 5
Substituindo os devidos valores
Calcularemos o módulo da seção
Passo 6
Calculando a tensão de flexão permitida.
Substituindo os valores
Resposta
Portanto, o valor mínimo de é de 100 mm.