Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Gere, Mecânica dos Materiais- Ed: 5º - Capítulo 1.2 - Ex. 6

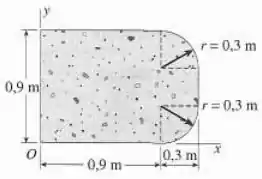
A seção transversal de um píer de concreto que está carregado uniformemente em compressão é mostrado na figura.

  1. Determine a tensão de compressão média σ c no concreto se a carga é igual a 7,5   M N .
  2. Determine as coordenadas x - e y - do ponto em que a carga resultante deve agir para produzir tensão normal uniforme.

Passo 1

Bora lá galera!

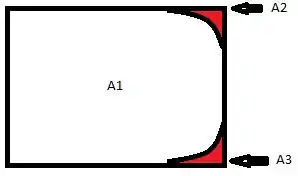
A 1 seria o retângulo todo, A 2 e A 3 seriam as áreas em vermelho.

P = 7,5   M N

Calculando a área do píer de concreto, temos que:

A 1 = 1,2 ⋅ 0,9 = 1,08   m 2

No Apêndice D, caso 12, ele nos mostra como calcular essas áreas A 2 e A 3 , logo:

A 2 = A 3 = 1 - π 4 ⋅ r 2 = 1 - π 4 ⋅ 0,3 2 = 0,019315   m 2  

Com isso my friends, a área do píer de concreto é:

A = A 1 - A 2 - A 3

A = 1,08 - 0,019315 - 0,019315

A = 1,0414   m 2

Passo 2

  1. Tendo a área, conseguimos calcular a tensão média σ c , logo:

    2. σ c = P A

    σ c = 7,5 1,0414

    σ c = 7,2018   M P a

  2. Agora a questão nos pede para calcular as coordenadas x - e y - em que a carga produz tensão normal uniforme, que justamente no centroide, logo:

Por simetria,

y - = 1 2 ( 0,9 ) = 0,45   m

Para o eixo x,

Área 1:

x 1 - = 1 2 ( 1,2 ) = 0,6   m

Área 2 e Área 3:

x 2 - = x 3 - = 0,9 + 2 r 3 ( 4 - π ) = 0,9 + 2 ⋅ 0,3 3 ⋅ ( 4 - π ) = 1,13299   m

Portanto,

x - = 1 A ⋅ x 1 - ⋅ A 1 - 2 ⋅ x 2 - ⋅ A 2

x - = 1 1,0414   ⋅ 0,6 ⋅ 1,08 - 2 ⋅ 1,13299 ⋅ 0,019315  

x - = 0,5802   m

Essa questão foi, heim... Bora pra próxima?

Resposta

  1. σ c = 7,2018   M P a
  2. x - = 0,5802   m

y - = 0,45   m

Resposta

Ei, a resposta está no passo a passo :)