Seis barras, todas de comprimento L, são unidas formando um tetraedro que está apoiado em uma superfície horizontal, sem atrito. Determine a força em cada barra quando uma força vertical P é aplicada em A.
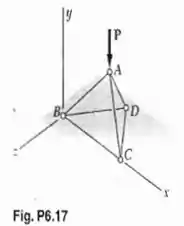
Passo 1
E ai seres de luz, tudo bem?
Bora resolver mais uma?
Encostaaa!!
Vamos considerar a vista do plano superior
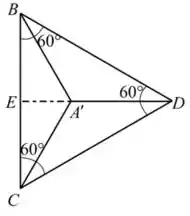
E a vista do plano .
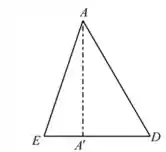
Passo 2
Cada lado do tetraedro é l
Da vista de cima do tetraedro, iremos encontrar o comprimento em BE
Iremos encontrar o comprimento de DE
O comprimento de EA’
O comprimento DA’
Partindo da vista do plano yz do tetraedro, encontraremos o comprimento AA’
Marcando as coordenadas de todas as juntas
Passo 3
Vamos considerar o diagrama de corpo livre no nó A
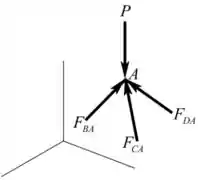
Vamos encontrar o vetor unitário de B a A
Vamos encontrar o vetor unitário de C a A
Vamos encontrar o vetor unitário de D a A
Representaremos a força externa que atua no nó A na forma cartesiana
Passo 4
Vamos aplicar a condição de equilíbrio de forças sobre o nó A
Igualando o coeficiente i a zero
Igualando o coeficiente j a zero
Igualando o coeficiente z a zero
Resolvendo as expressões , temos os valores nos cabos
Portanto, as forças nos cabos AB, AC, e AD são , respectivamente.
Passo 5
Considerando o D.C.L do nó B
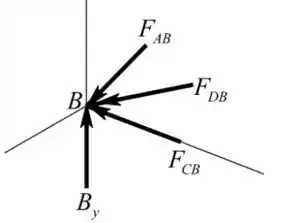
Vamos encontrar o vetor unitário de A a B
Vamos encontrar o vetor unitário de C a B
Vamos encontrar o vetor unitário de D a B
Representaremos a força externa que atua no nó B na forma cartesiana
Vamos aplicar a condição de equilíbrio de forças sobre o nó B
Igualando o coeficiente z a zero
O sinal negativo informa que o membro está sendo tracionado.
Igualando o coeficiente i a zero
O sinal negativo informa que o membro está sendo tracionado.
Portanto, as forças nos cabos BD e BC são , respectivamente.
Passo 6
Considerando o diagrama de corpo livre no nó C
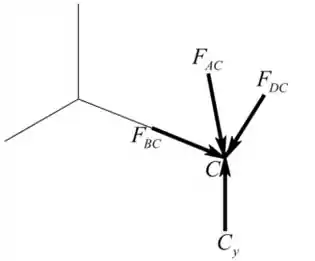
Vamos encontrar o vetor unitário de A a C
Vamos encontrar o vetor unitário de B a C
Vamos encontrar o vetor unitário de D a C
Representaremos a força externa que atua no nó C na forma cartesiana
Vamos aplicar a condição de equilíbrio de forças sobre o nó C
Igualando o coeficiente z a zero
O sinal negativo informa que o membro está sendo tracionado.
Portanto, as forças nos cabos CD são .
Resposta
Portanto, as forças nos cabos AB, AC, e AD são , respectivamente.
Portanto, as forças nos cabos BD e BC são , respectivamente.
Portanto, as forças nos cabos CD são .