Solucione O Problema P8.18 usando o método da viga conjugada.
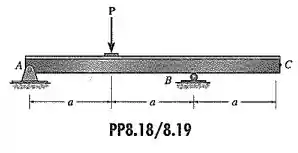
Passo 1
Saaaalve, tranquilo? Vamos lá resolver mais uma questão juntos?! 😊
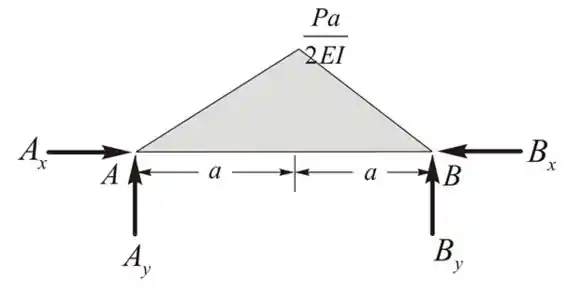
O diagrama de corpo livre da viga é considerado da seguinte maneira
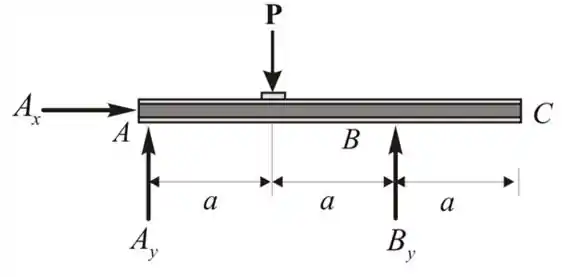
Vamos considerar as condições de equilíbrio, e aplicaremos o momento em torno de A
Aplicando a condição de equilíbrio vertical
Passo 2
Desenhando o diagrama de momento fletor da viga
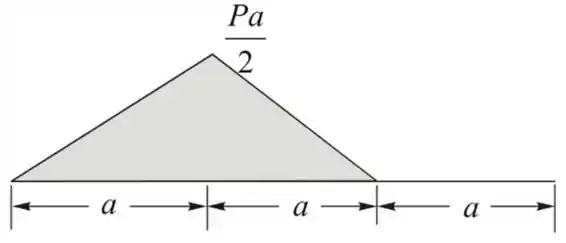
O feixe conjugado:
O diagrama de momento fletor da viga real
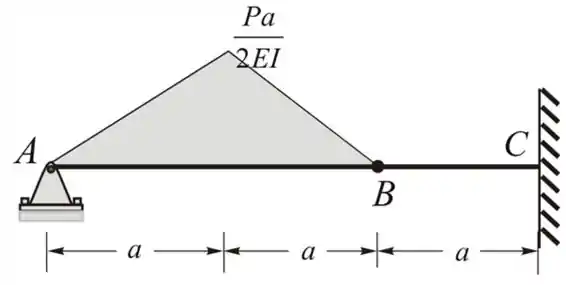
Temos as reações
Passo 3
Vamos considerar as condições de equilíbrio, e aplicaremos o momento em torno de A
Vamos considerar
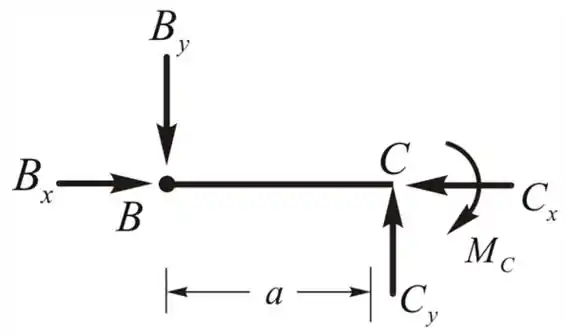
Vamos aplicar a condição de equilíbrio vertical
Aplicando o momento em C
Passo 4
A inclinação em C na viga real = força de cisalhamento em C na viga conjugada
Deflexão em C na viga real = Momento fletor em C na viga conjugada.