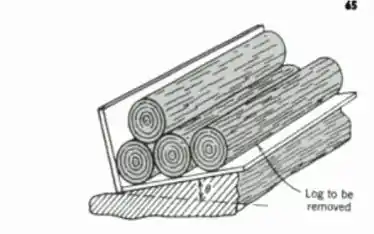
Suponha que toras idênticas, lisas e sem atrito sejam empilhadas em um caminhão baú (lados perpendiculares ao fundo). O caminhão é forçado para fora da rodovia e para em uma quilha uniforme no sentido do comprimento, mas com a caçamba formando um ângulo θ com a horizontal, conforme mostrado. Quando o caminhão é descarregado, qual é o menor ângulo para θ para que, quando a quarta tora for removida, as três toras restantes permaneçam onde estão?
Passo 1
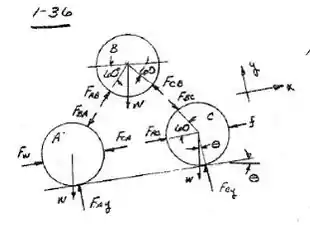
Suponha que OS LOGS TENHAM TODOS O MESMO DIÂMETRO
Quando C está sob movimento
Para C,
Passo 2
Para B
Resolvendo para