Trabalhe novamente com o problema no Exemplo 13.1 no caso de o ponto arrancado estar a uma distância L/3 de uma extremidade. Comente sobre a natureza dos modos permitidos.
Passo 1
E aí pessoal, belezinha? Vamos trabalhar agora em algumas questões de sistemas contínuos; ondas.
Do enunciado temos o esquema do problema:
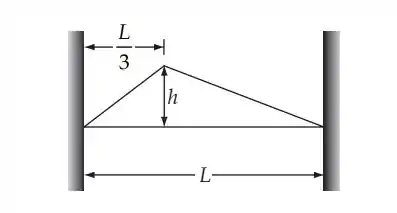
As condições iniciais são:
Como , todos os νr desaparecem. Os µr são dados por:
Vemos que µr = 0 para r = 3, 6, 9, etc. A função de deslocamento é:
Onde:
As freqüências ω3, ω6, ω9, etc. estão ausentes porque o deslocamento inicial em L/3 impede que esse ponto seja um nó. Assim, nenhum dos harmônicos com um nó em L/3 é excitado.
Resposta
Ver passo a passo.