Trace os diagramas de força corta cortante e momento fletor para a viga AB.
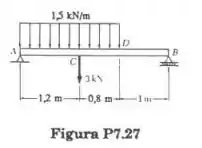
Passo 1
E ai seres de luz, tudo bem?
Bora resolver mais uma?
Encostaaa!!
Diagrama de corpo livre da viga
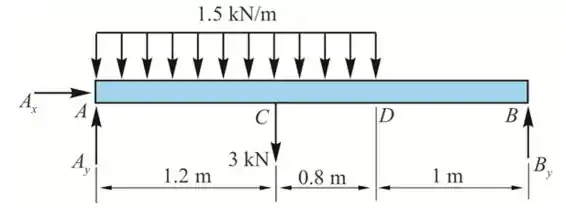
Tomando os momentos sobre A
Da equação de equilíbrio ao longo do eixo y
Da equação de equilíbrio ao longo do eixo x
Passo 2
Considerando uma seção entre AC a uma distância x de A
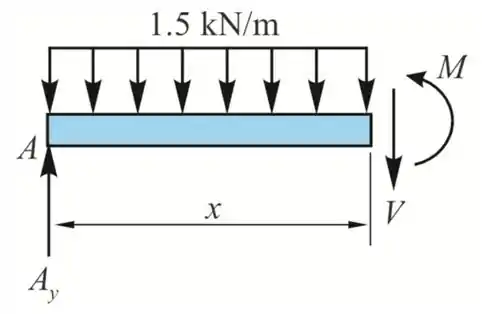
Da equação de equilíbrio ao longo do eixo y
Tomemos momentos sobre a seção
Em
Em
Passo 3
Considerando uma seção entre CD a uma distância x de A
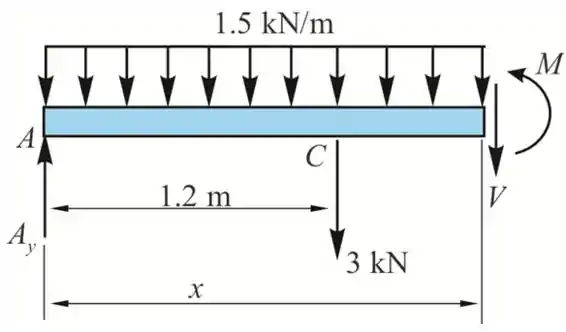
Da equação de equilíbrio ao longo do eixo y
Tomemos momentos sobre a seção
Em
Em
Passo 4
Considerando uma seção entre BD a uma distância x de B
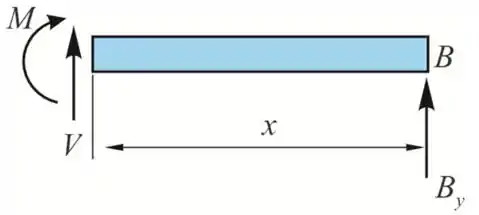
Da equação de equilíbrio ao longo do eixo y
Tomemos momentos sobre a seção
Em
Em
Passo 5
Diagrama Fletor e cortante
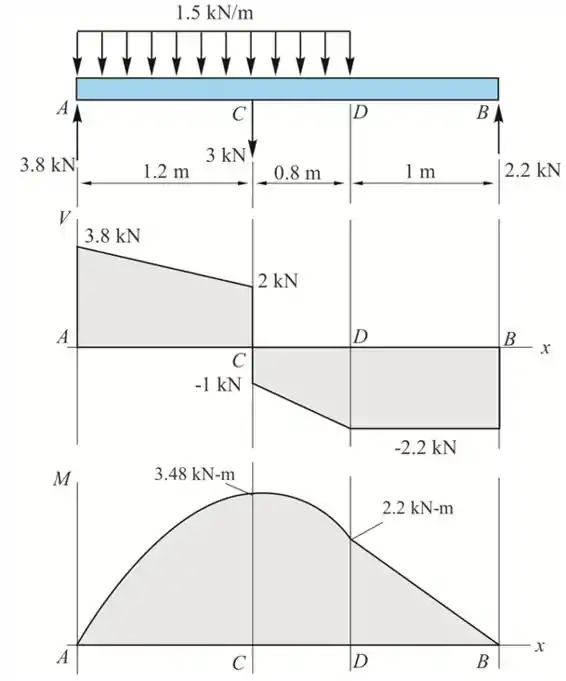
Resposta
Vide o passo a passo.