Trace os diagramas de força cortante e momento fletor para a viga e o carregamento da figura.
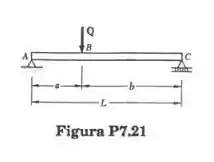
Passo 1
Boraaa galerinha, aniimaaa, vamos resolver mais um!!
Só bora então!!
Observação , Show?
Digrama de corpo livre da viga
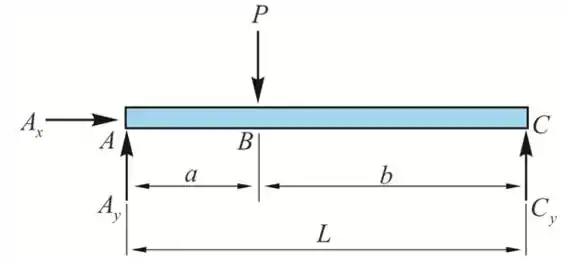
Passo 2
Tomemos momentos sobre B
Da equação de equilíbrio ao longo do eixo x, temos
Da equação de equilíbrio ao longo do eixo y
Passo 3
Considerando uma seção entre AB a uma distância x de A, temos
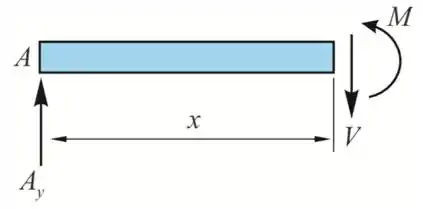
Pela equação de equilíbrio ao longo do eixo y, temos
Tomemos momentos sobre a seção
Em
Em
Passo 4
Considerando uma seção entre BC a uma distância x de A
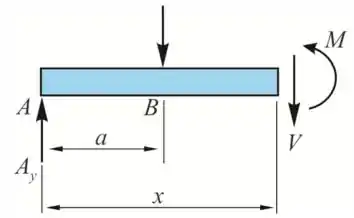
Da equação de equilíbrio ao longo do eixo y
Passo 5
Tomando momentos sobre a seção
Em
Em
Passo 6
Temos agora os diagramas de cortante e momento fletor
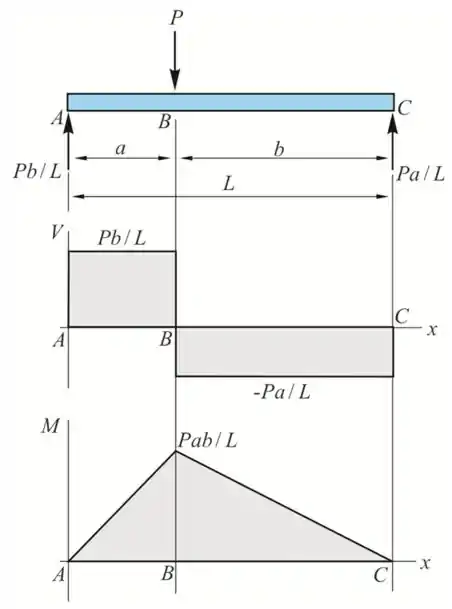
Resposta
Vide o passo a passo.