Trace os diagramas de força cortante e momento fletor para a viga e o carregamento da figura.
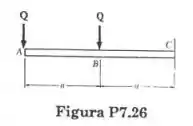
Passo 1
Falaiii meus xuxu’s, ceis tão bonzinho??
Espero que sim hein, bora lá pra mais uma?
Encostaaaa
Bora, bora no D.C.L
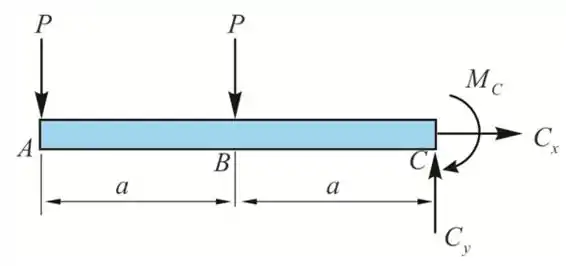
Pela equação de equilíbrio ao longo do eixo de x, temos
Pela equação de equilíbrio ao longo do eixo de y, temos
Tomemos momentos sobre C
Passo 2
Considerando uma seção entre AB a uma distância x de A
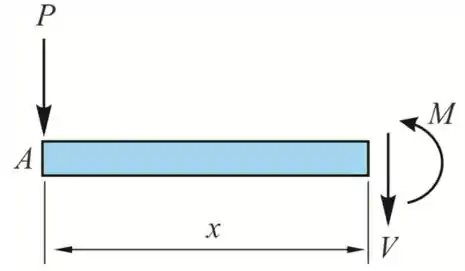
Pela equação de equilíbrio ao longo do eixo de y, temos
Tomemos momentos sobre a seção
Em
Em
Passo 3
Considerando uma seção entre BC a uma distancia x de A
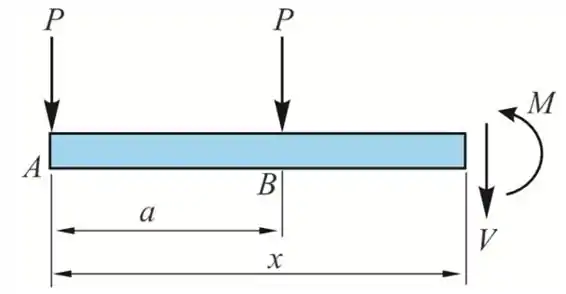
Pela equação de equilíbrio ao longo do eixo de y, temos
Tomemos momentos sobre a seção
Em
Em
Passo 4
Diagrama de Fletor e cortante.
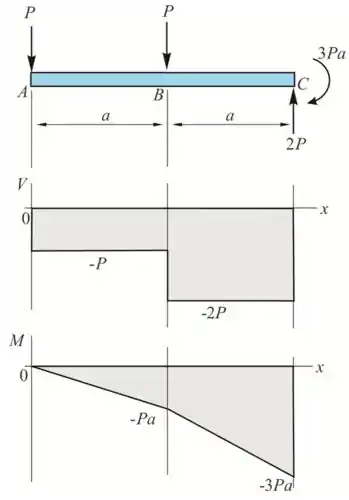
Resposta
Vide o passo a passo.