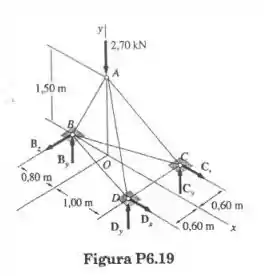
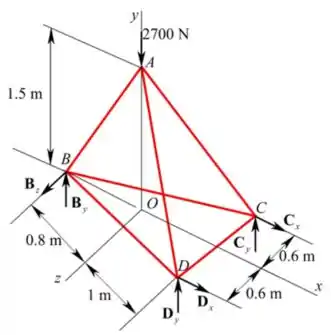
A treliça tridimensional está apoiada nas seis reações da figura. Se uma carga vertical de é aplicada em A, determine (a) as reações e (b) a força em cada barra.
Passo 1
Falaiii meus xuxu’s, ceis tão bonzinho??
Espero que sim hein, bora lá pra mais uma?
Encostaaaa
Vamos inicias desenhando o diagrama de corpo livre da treliça conforme mostrado a seguir:
Passo 2
- Calcularemos o vetor unitário de CD da seguinte maneira
- Iremos desenhar o diagrama de corpo livre do ponto D como mostra a figura a seguir
Agora iremos calcular as reações aplicando a equação de equilíbrio da seguinte maneira
Substituindo
Portanto, a reação em B, .
Calculando as reações aplicando a equação de equilíbrio da seguinte maneira
Portanto, a reação em B,
Passo 3
Agora iremos calcular as reações aplicando a equação de equilíbrio da seguinte maneira
Substituindo
Igualando a componente j da seguinte maneira :
Igualando a componente i da seguinte maneira :
Portanto, a reação em C, e
Calculando as reações aplicando a equação de equilíbrio da seguinte maneira
Calculando as reações aplicando a equação de equilíbrio da seguinte maneira
Portanto, a reação em D, e
Passo 4
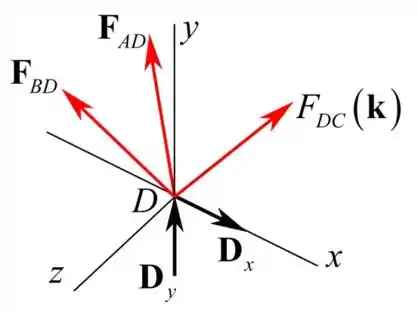
Vamos calcular a força AD da seguinte maneira
Calculando a força BD da seguinte maneira
Calculando a força no membro AD aplicando a equação de equilíbrio para o nó D como mostra a seguir:
Substituindo
Portanto, a força no membro AD, .
Calculando a força no membro BD aplicando a equação de equilíbrio para o nó D como mostra a seguir:
Substituindo
Portanto, a força no membro BD, .
Calculando a força no membro DC aplicando a equação de equilíbrio para o nó D como mostra a seguir:
Substituindo
Portanto, a força no membro DC, .
Passo 3
Vamos desenhar o diagrama de corpo livre como mostra a figura a seguir na junta C.
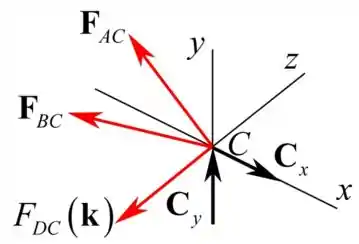
Vamos calcular a força AC da seguinte maneira
Calculando a força BC da seguinte maneira
Calculando a força no membro AC aplicando a equação de equilíbrio para o nó C como mostra a seguir:
Substituindo
Portanto, a força no membro AC, .
Calculando a força no membro BC aplicando a equação de equilíbrio para o nó C como mostra a seguir:
Substituindo
Portanto, a força no membro BD, .
Passo 4
Vamos desenhar o diagrama de corpo livre como mostra a figura a seguir na junta B.
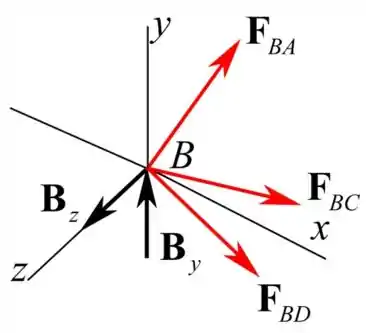
Vamos calcular a força BD da seguinte maneira
Vamos calcular a força BC da seguinte maneira
Vamos calcular a força BA da seguinte maneira
Vamos calcular a força no membro AB aplicando a equação de equilíbrio para o nó B como mostra a seguir
Substituindo
Portanto, a força no membro BA, .
Resposta
- Portanto, a reação em B, .
- Portanto, a força no membro AD, .
Portanto, a reação em B, .
Portanto, a reação em C, e .
Portanto, a reação em D, e .
Portanto, a força no membro BD, .
Portanto, a força no membro DC, .
Portanto, a força no membro AC, .
Portanto, a força no membro BA, .