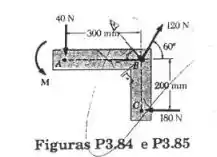
As três forças da figura e um binário de momento M são aplicados a um suporte. Determine o momento do binário sabendo que a linha de ação da resultante do sistema de forças deve passar pelo ponto (a) A, (b) B, (c) C.
Passo 1
Falaiii meus xuxu’s, ceis tão bonzinho??
Espero que sim hein, bora lá pra mais uma?
Encostaaaa
- A carga equivalente
- Carga equivalente
- Carga equivalente
Passo 2
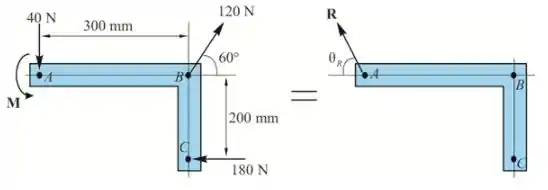
A componente x da força resultante R
A componente y da força resultante R:
O ângulo formado pela força resultante
A soma dos momentos em relação ao ponto A deve ser a mesma para ambos os casos
Portanto, o momento binário em A é .
Passo 3
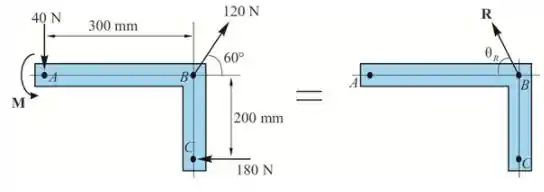
A componente x da força resultante R
A componente y da força resultante R:
O ângulo formado pela força resultante
A soma dos momentos em relação ao ponto A deve ser a mesma para ambos os casos
Portanto, o momento binário em A é .
Passo 4
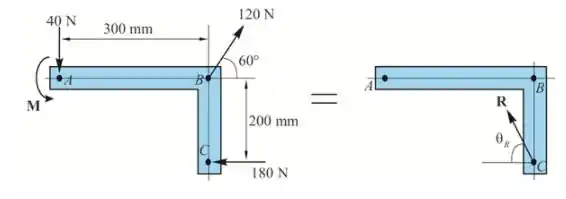
A componente x da força resultante R
A componente y da força resultante R:
O ângulo formado pela força resultante
A soma dos momentos em relação ao ponto A deve ser a mesma para ambos os casos
Portanto, o momento binário em A é .
Resposta
- Portanto, o momento binário em A é .
- Portanto, o momento binário em A é .
- Portanto, o momento binário em A é .