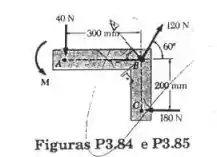
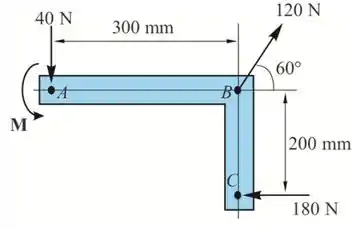
As três forças da figura e um binário de torque de módulo são aplicados a um suporte .(a) Determine a resultante desse sistema de forças. (b) Determine os pontos onde a linha de ação da resultante corta as retas AB e BC.
Passo 1
Boraaa galerinha, aniimaaa, vamos resolver mais um!!
Só bora então!!
Já iremos iniciar com o dado do nosso carregamento
Passo 2
- Dado que
- Carga equivalente :
A componente x da força resultante R:
A componente y da força resultante R:
O ângulo formado pela força resultante
A magnitude da força resultante R:
Portanto, a força resultante das três forças dadas é
Passo 3
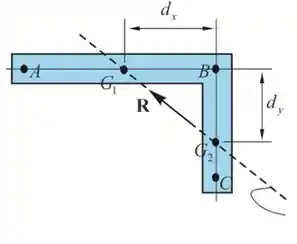
Vamos considerar que a força resultante está agindo no ponto .
A soma dos momentos em relação ao ponto B deve ser a mesma para ambos os casos
Portanto, a força resultante intercepta a linha AB em à esquerda do ponto B.
Considerando que a força resultante está agindo no ponto .
A soma dos momentos em relação ao ponto B deve ser a mesma para ambos os casos
Portanto, a força resultante intercepta a linha BC em para baixo do ponto B.
Resposta
- Portanto, a força resultante das três forças dadas é
- Portanto, a força resultante intercepta a linha AB em à esquerda do ponto B.
Portanto, a força resultante intercepta a linha BC em para baixo do ponto B.