Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 13.Problemas - Ex. 129
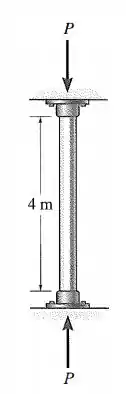
O tubo de aço está engastado em ambas as extremidades. Se tiver de comprimento e diâmetro externo de , determine a espessura exigida para que possa suportar uma carga axial sem sofrer flambagem. e .
Passo 1
Fala aí pessoal, vamos para mais um exercício de resmat. O enunciado quer a espessura da parede do tubo, para que ele suporte uma carga de 100kN sem flambar. Quando a gente fala de suportar sem flambar, a gente ta falando da carga crítica. Então qual a espessura da parede, para que a carga crítica seja de pelo menos 100kN?
Pra relacionar as incógnitas que a gente tem e as que a gente quer, vamos usar a fórmula pra carga crítica:
A gente já tem:
Presta atenção em quais tem que ser as unidades!
Pelo tubo estar engastado nas extremidades:
Então só ficou faltando o momento de inércia, que é onde vai aparecer a espessura da parede! A equação do momento de inércia para um tubo é dada por :
A espessura da parede é a diferença entre o raio externo Re e o raio interno Ri.
Passo 2
Agora que temos todos os valores e a fórmula pro momento de inércia, vamos substituir na expressão da carga crítica.
Passo 3
Por fim, para sabermos se a carga de 100kN é realmente aceitável, precisamos verificar se a tensão causada por essa força não excede a tensão de escoamento do material. Mesmo que o enunciado não tenha pedido isso diretamente, é sempre bom fazer porque não adianta nada se a coluna não flambar, se ela escoa. Além disso, embora não tenha sido pedido diretamente, o enunciado deu pra gente o valor da tensão de escoamento do material, que só serve pra isso mesmo. Então já é uma dica que é pra fazer!
A tensão crítica é:
Portanto, como , este valor antende as limites de escoamento.