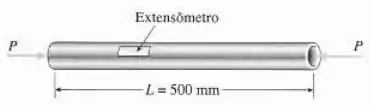
Um tubo circular de alumínio de comprimento é carregado em compressão por forças (veja a figura). Os diâmetros externo e interno têm e , respectivamente. Um medidor de deformação é colocado na superfície externa da barra para medir deformações normais na direção longitudinal.
- Se a deformação medida é , qual é o encurtamento da barra?
- Se a tensão de compressão na barra deve ser de , qual deveria ser a carga ?
Passo 1
Dados:
Bora lá galera!
- Para calcular o encurtamento da barra, basta multiplicarmos a deformação pelo comprimento, logo:
- Para uma tensão de , a carga será:
Com isso my friends, podemos finalmente calcular a carga , logo:
Essa questão foi, heim... Bora pra próxima?